Attacking Adversarial Defences by Smoothing the Loss Landscape
Paper and Code
Aug 05, 2022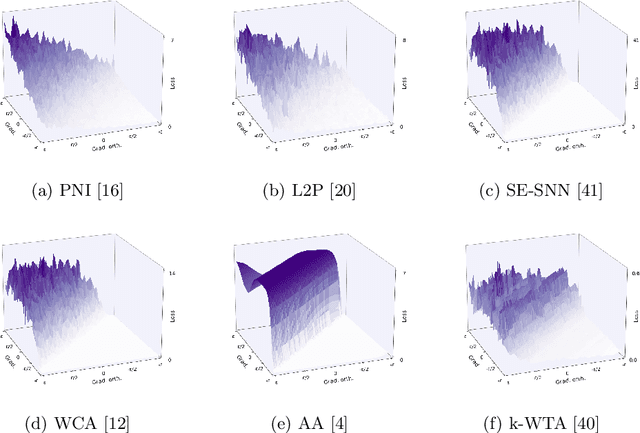
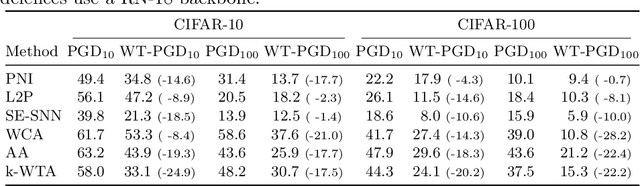
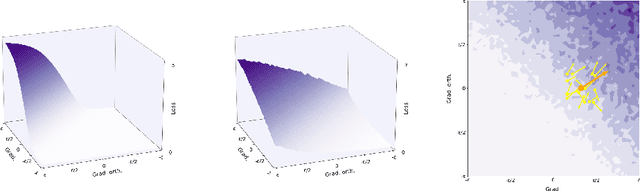
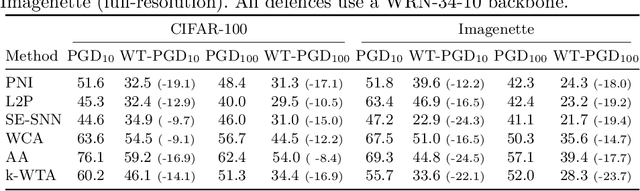
This paper investigates a family of methods for defending against adversarial attacks that owe part of their success to creating a noisy, discontinuous, or otherwise rugged loss landscape that adversaries find difficult to navigate. A common, but not universal, way to achieve this effect is via the use of stochastic neural networks. We show that this is a form of gradient obfuscation, and propose a general extension to gradient-based adversaries based on the Weierstrass transform, which smooths the surface of the loss function and provides more reliable gradient estimates. We further show that the same principle can strengthen gradient-free adversaries. We demonstrate the efficacy of our loss-smoothing method against both stochastic and non-stochastic adversarial defences that exhibit robustness due to this type of obfuscation. Furthermore, we provide analysis of how it interacts with Expectation over Transformation; a popular gradient-sampling method currently used to attack stochastic defences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge