Asynchronous Stochastic Proximal Methods for Nonconvex Nonsmooth Optimization
Paper and Code
Sep 15, 2018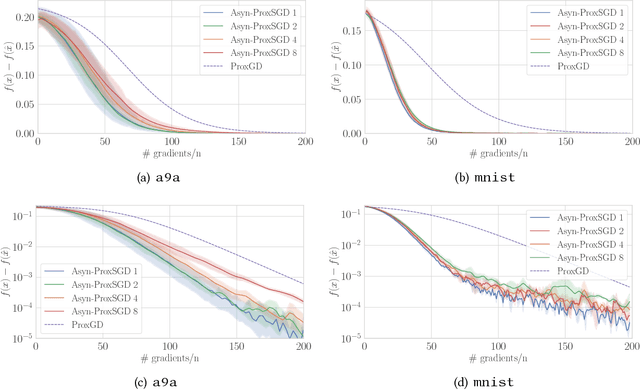

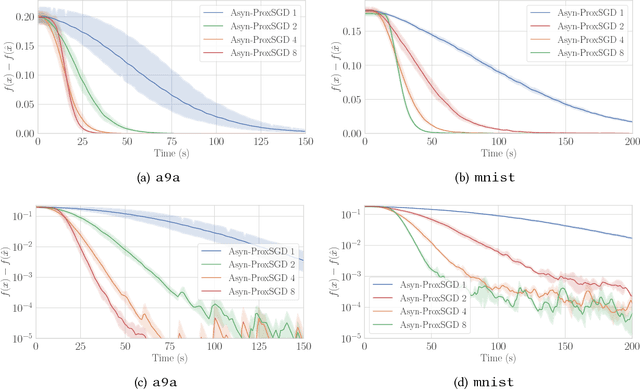

We study stochastic algorithms for solving nonconvex optimization problems with a convex yet possibly nonsmooth regularizer, which find wide applications in many practical machine learning applications. However, compared to asynchronous parallel stochastic gradient descent (AsynSGD), an algorithm targeting smooth optimization, the understanding of the behavior of stochastic algorithms for nonsmooth regularized optimization problems is limited, especially when the objective function is nonconvex. To fill this theoretical gap, in this paper, we propose and analyze asynchronous parallel stochastic proximal gradient (Asyn-ProxSGD) methods for nonconvex problems. We establish an ergodic convergence rate of $O(1/\sqrt{K})$ for the proposed Asyn-ProxSGD, where $K$ is the number of updates made on the model, matching the convergence rate currently known for AsynSGD (for smooth problems). To our knowledge, this is the first work that provides convergence rates of asynchronous parallel ProxSGD algorithms for nonconvex problems. Furthermore, our results are also the first to show the convergence of any stochastic proximal methods without assuming an increasing batch size or the use of additional variance reduction techniques. We implement the proposed algorithms on Parameter Server and demonstrate its convergence behavior and near-linear speedup, as the number of workers increases, on two real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge