Asymptotically Fair Participation in Machine Learning Models: an Optimal Control Perspective
Paper and Code
Nov 16, 2023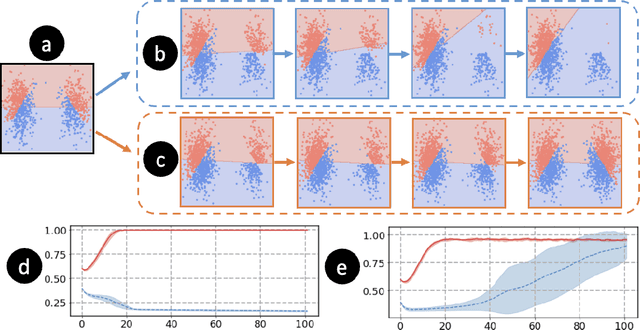

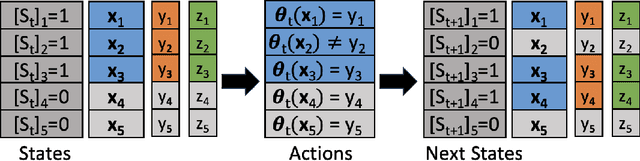

The performance of state-of-the-art machine learning models often deteriorates when testing on demographics that are under-represented in the training dataset. This problem has predominately been studied in a supervised learning setting where the data distribution is static. However, real-world applications often involve distribution shifts caused by the deployed models. For instance, the performance disparity against monitory users can lead to a high customer churn rate, thus the available data provided by active users are skewed due to the lack of minority users. This feedback effect further exacerbates the disparity among different demographic groups in future steps. To address this issue, we propose asymptotically fair participation as a condition to maintain long-term model performance over all demographic groups. In this work, we aim to address the problem of achieving asymptotically fair participation via optimal control formulation. Moreover, we design a surrogate retention system based on existing literature on evolutionary population dynamics to approximate the dynamics of distribution shifts on active user counts, from which the objective of achieving asymptotically fair participation is formulated as an optimal control problem, and the control variables are considered as the model parameters. We apply an efficient implementation of Pontryagin's maximum principle to estimate the optimal control solution. To evaluate the effectiveness of the proposed method, we design a generic simulation environment that simulates the population dynamics of the feedback effect between user retention and model performance. When we deploy the resulting models to the simulation environment, the optimal control solution accounts for long-term planning and leads to superior performance compared with existing baseline methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge