Assignment Algorithms for Multi-Robot Multi-Target Tracking with Sufficient and Limited Sensing Capability
Paper and Code
Mar 08, 2023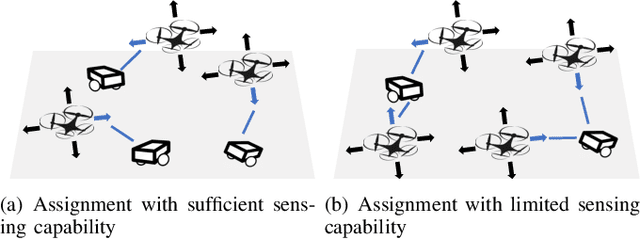
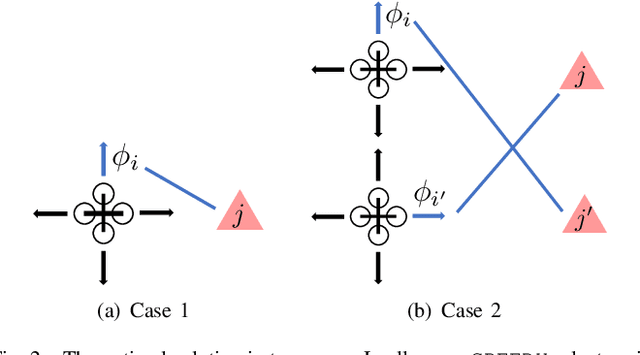
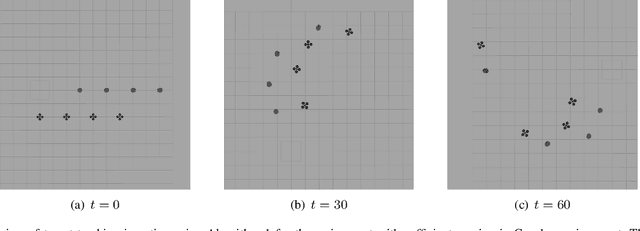
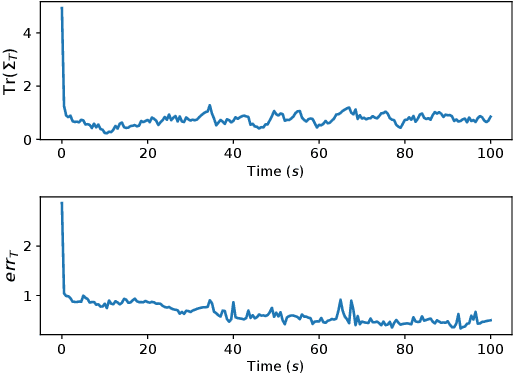
We study the problem of assigning robots with actions to track targets. The objective is to optimize the robot team's tracking quality which can be defined as the reduction in the uncertainty of the targets' states. Specifically, we consider two assignment problems given the different sensing capabilities of the robots. In the first assignment problem, a single robot is sufficient to track a target. To this end, we present a greedy algorithm (Algorithm 1) that assigns a robot with its action to each target. We prove that the greedy algorithm has a 1/2 approximation bound and runs in polynomial time. Then, we study the second assignment problem where two robots are necessary to track a target. We design another greedy algorithm (Algorithm 2) that assigns a pair of robots with their actions to each target. We prove that the greedy algorithm achieves a 1/3 approximation bound and has a polynomial running time. Moreover, we illustrate the performance of the two greedy algorithms in the ROS-Gazebo environment where the tracking patterns of one robot following one target using Algorithm 1 and two robots following one target using Algorithm 2 are clearly observed. Further, we conduct extensive comparisons to demonstrate that the two greedy algorithms perform close to their optimal counterparts and much better than their respective (1/2 and 1/3) approximation bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge