Are All Edges Necessary? A Unified Framework for Graph Purification
Paper and Code
Nov 09, 2022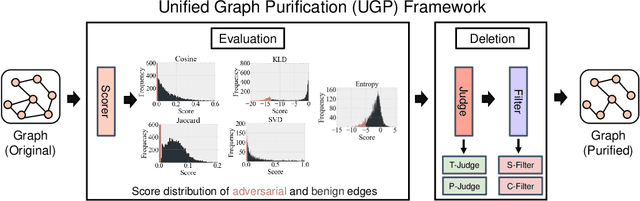
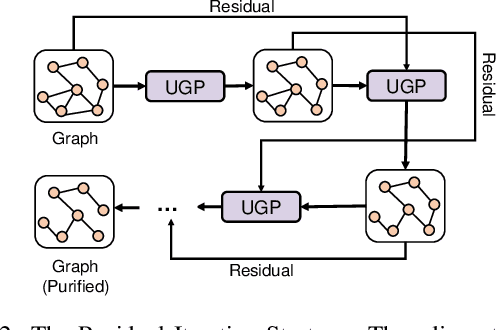

Graph Neural Networks (GNNs) as deep learning models working on graph-structure data have achieved advanced performance in many works. However, it has been proved repeatedly that, not all edges in a graph are necessary for the training of machine learning models. In other words, some of the connections between nodes may bring redundant or even misleading information to downstream tasks. In this paper, we try to provide a method to drop edges in order to purify the graph data from a new perspective. Specifically, it is a framework to purify graphs with the least loss of information, under which the core problems are how to better evaluate the edges and how to delete the relatively redundant edges with the least loss of information. To address the above two problems, we propose several measurements for the evaluation and different judges and filters for the edge deletion. We also introduce a residual-iteration strategy and a surrogate model for measurements requiring unknown information. The experimental results show that our proposed measurements for KL divergence with constraints to maintain the connectivity of the graph and delete edges in an iterative way can find out the most edges while keeping the performance of GNNs. What's more, further experiments show that this method also achieves the best defense performance against adversarial attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge