ARC -- Actor Residual Critic for Adversarial Imitation Learning
Paper and Code
Jun 05, 2022
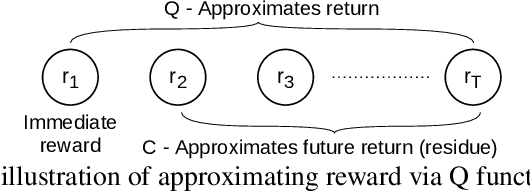
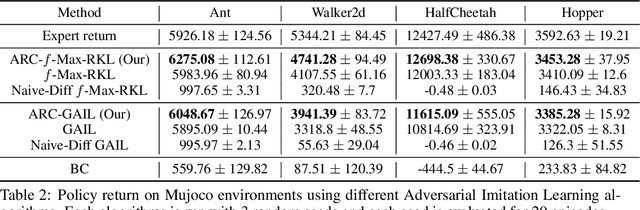
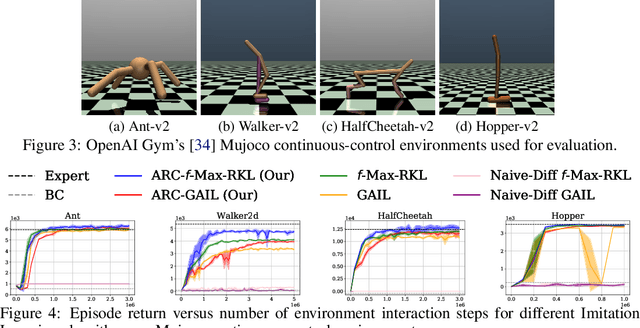
Adversarial Imitation Learning (AIL) is a class of popular state-of-the-art Imitation Learning algorithms where an artificial adversary's misclassification is used as a reward signal and is optimized by any standard Reinforcement Learning (RL) algorithm. Unlike most RL settings, the reward in AIL is differentiable but model-free RL algorithms do not make use of this property to train a policy. In contrast, we leverage the differentiability property of the AIL reward function and formulate a class of Actor Residual Critic (ARC) RL algorithms that draw a parallel to the standard Actor-Critic (AC) algorithms in RL literature and uses a residual critic, C function (instead of the standard Q function) to approximate only the discounted future return (excluding the immediate reward). ARC algorithms have similar convergence properties as the standard AC algorithms with the additional advantage that the gradient through the immediate reward is exact. For the discrete (tabular) case with finite states, actions, and known dynamics, we prove that policy iteration with $C$ function converges to an optimal policy. In the continuous case with function approximation and unknown dynamics, we experimentally show that ARC aided AIL outperforms standard AIL in simulated continuous-control and real robotic manipulation tasks. ARC algorithms are simple to implement and can be incorporated into any existing AIL implementation with an AC algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge