Approximation Algorithms for Active Sequential Hypothesis Testing
Paper and Code
Mar 07, 2021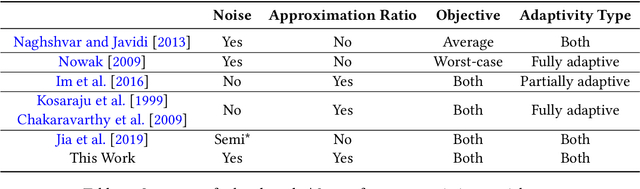
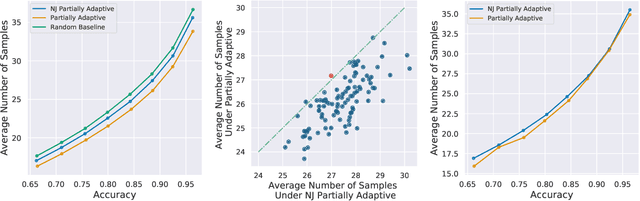
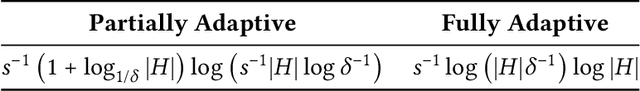
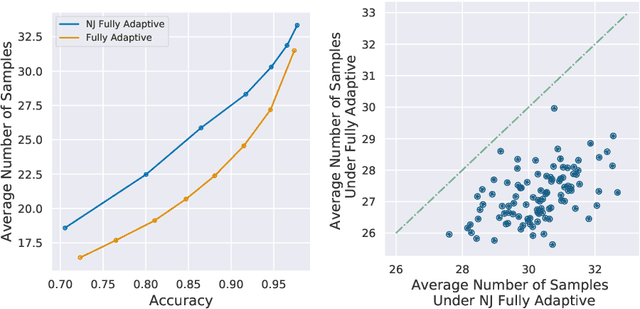
In the problem of active sequential hypotheses testing (ASHT), a learner seeks to identify the true hypothesis $h^*$ from among a set of hypotheses $H$. The learner is given a set of actions and knows the outcome distribution of any action under any true hypothesis. While repeatedly playing the entire set of actions suffices to identify $h^*$, a cost is incurred with each action. Thus, given a target error $\delta>0$, the goal is to find the minimal cost policy for sequentially selecting actions that identify $h^*$ with probability at least $1 - \delta$. This paper provides the first approximation algorithms for ASHT, under two types of adaptivity. First, a policy is partially adaptive if it fixes a sequence of actions in advance and adaptively decides when to terminate and what hypothesis to return. Under partial adaptivity, we provide an $O\big(s^{-1}(1+\log_{1/\delta}|H|)\log (s^{-1}|H| \log |H|)\big)$-approximation algorithm, where $s$ is a natural separation parameter between the hypotheses. Second, a policy is fully adaptive if action selection is allowed to depend on previous outcomes. Under full adaptivity, we provide an $O(s^{-1}\log (|H|/\delta)\log |H|)$-approximation algorithm. We numerically investigate the performance of our algorithms using both synthetic and real-world data, showing that our algorithms outperform a previously proposed heuristic policy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge