Approximate Principal Direction Trees
Paper and Code
Jun 18, 2012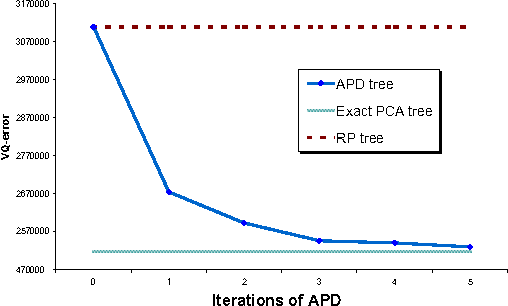

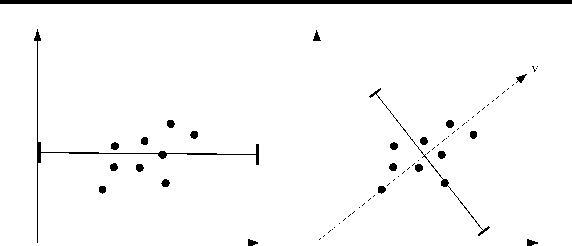
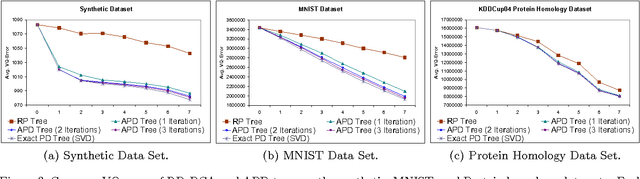
We introduce a new spatial data structure for high dimensional data called the \emph{approximate principal direction tree} (APD tree) that adapts to the intrinsic dimension of the data. Our algorithm ensures vector-quantization accuracy similar to that of computationally-expensive PCA trees with similar time-complexity to that of lower-accuracy RP trees. APD trees use a small number of power-method iterations to find splitting planes for recursively partitioning the data. As such they provide a natural trade-off between the running-time and accuracy achieved by RP and PCA trees. Our theoretical results establish a) strong performance guarantees regardless of the convergence rate of the power-method and b) that $O(\log d)$ iterations suffice to establish the guarantee of PCA trees when the intrinsic dimension is $d$. We demonstrate this trade-off and the efficacy of our data structure on both the CPU and GPU.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge