Approximate matrix completion based on cavity method
Paper and Code
Jun 29, 2019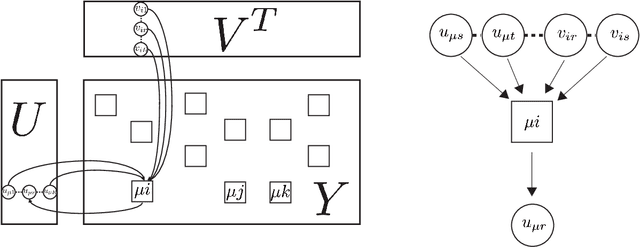

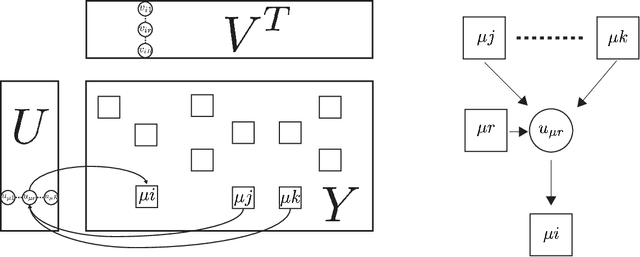
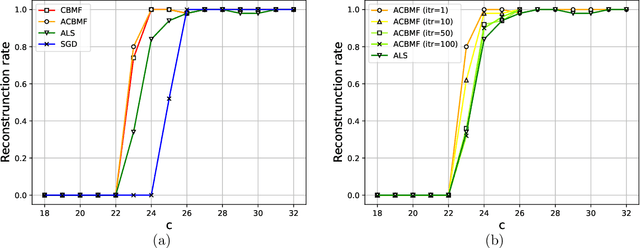
In order to solve large matrix completion problems with practical computational cost, an approximate approach based on matrix factorization has been widely used. Alternating least squares (ALS) and stochastic gradient descent (SGD) are two major algorithms to this end. In this study, we propose a new algorithm, namely cavity-based matrix factorization (CBMF) and approximate cavity-based matrix factorization (ACBMF), which are developed based on the cavity method from statistical mechanics. ALS yields solutions with less iterations when compared to those of SGD. This is because its update rules are described in a closed form although it entails higher computational cost. CBMF can also write its update rules in a closed form, and its computational cost is lower than that of ALS. ACBMF is proposed to compensate a disadvantage of CBMF in terms of relatively high memory cost. We experimentally illustrate that the proposed methods outperform the two existing algorithms in terms of convergence speed per iteration, and it can work under the condition where observed entries are relatively fewer. Additionally, in contrast to SGD, (A)CBMF does not require scheduling of the learning rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge