Approximate Inference with the Variational Holder Bound
Paper and Code
Jun 19, 2015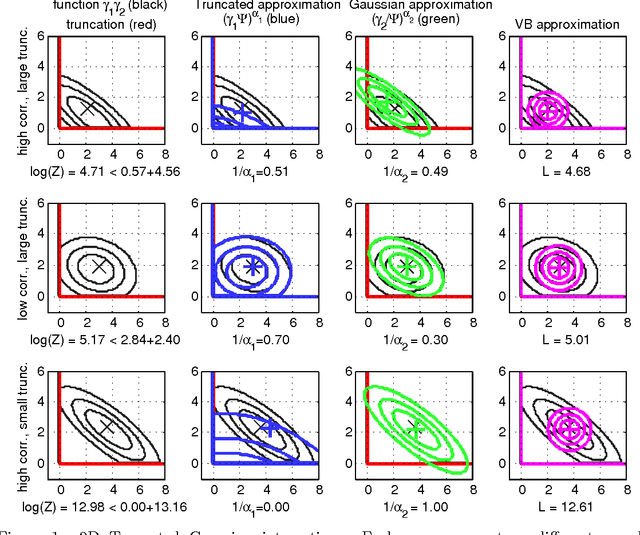

We introduce the Variational Holder (VH) bound as an alternative to Variational Bayes (VB) for approximate Bayesian inference. Unlike VB which typically involves maximization of a non-convex lower bound with respect to the variational parameters, the VH bound involves minimization of a convex upper bound to the intractable integral with respect to the variational parameters. Minimization of the VH bound is a convex optimization problem; hence the VH method can be applied using off-the-shelf convex optimization algorithms and the approximation error of the VH bound can also be analyzed using tools from convex optimization literature. We present experiments on the task of integrating a truncated multivariate Gaussian distribution and compare our method to VB, EP and a state-of-the-art numerical integration method for this problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge