Analyzing the Capacity of Distributed Vector Representations to Encode Spatial Information
Paper and Code
Sep 30, 2020
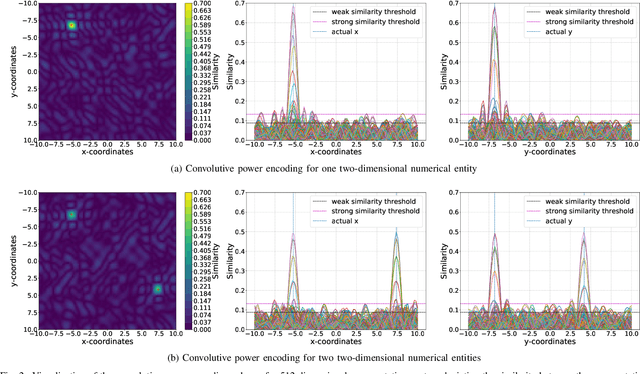
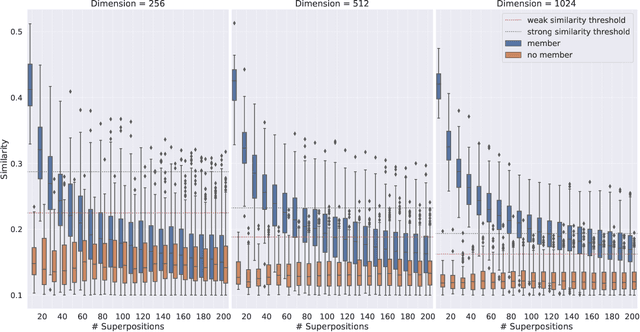
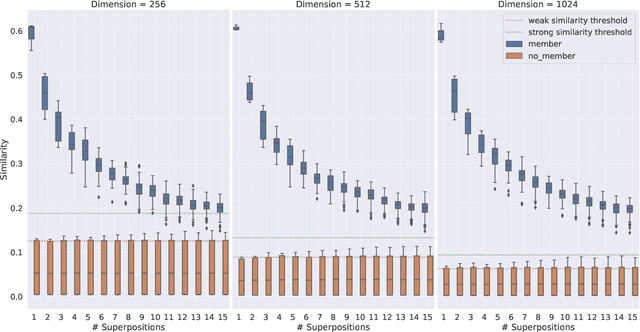
Vector Symbolic Architectures belong to a family of related cognitive modeling approaches that encode symbols and structures in high-dimensional vectors. Similar to human subjects, whose capacity to process and store information or concepts in short-term memory is subject to numerical restrictions,the capacity of information that can be encoded in such vector representations is limited and one way of modeling the numerical restrictions to cognition. In this paper, we analyze these limits regarding information capacity of distributed representations. We focus our analysis on simple superposition and more complex, structured representations involving convolutive powers to encode spatial information. In two experiments, we find upper bounds for the number of concepts that can effectively be stored in a single vector.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge