Analytic Marching: An Analytic Meshing Solution from Deep Implicit Surface Networks
Paper and Code
Feb 16, 2020
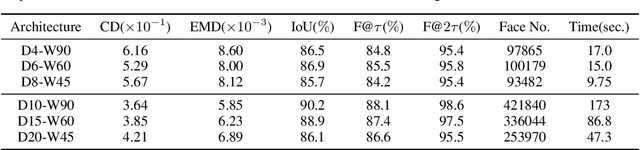
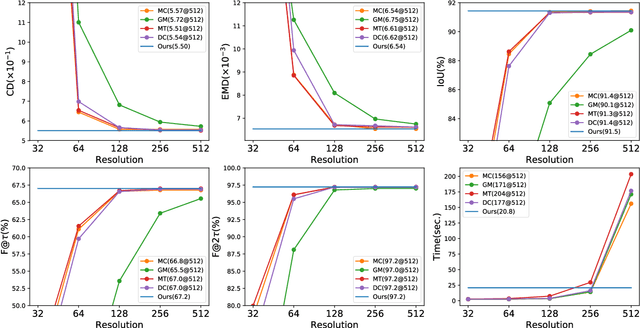

This paper studies a problem of learning surface mesh via implicit functions in an emerging field of deep learning surface reconstruction, where implicit functions are popularly implemented as multi-layer perceptrons (MLPs) with rectified linear units (ReLU). To achieve meshing from learned implicit functions, existing methods adopt the de-facto standard algorithm of marching cubes; while promising, they suffer from loss of precision learned in the MLPs, due to the discretization nature of marching cubes. Motivated by the knowledge that a ReLU based MLP partitions its input space into a number of linear regions, we identify from these regions analytic cells and analytic faces that are associated with zero-level isosurface of the implicit function, and characterize the theoretical conditions under which the identified analytic faces are guaranteed to connect and form a closed, piecewise planar surface. Based on our theorem, we propose a naturally parallelizable algorithm of analytic marching, which marches among analytic cells to exactly recover the mesh captured by a learned MLP. Experiments on deep learning mesh reconstruction verify the advantages of our algorithm over existing ones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge