An Unbiased Risk Estimator for Learning with Augmented Classes

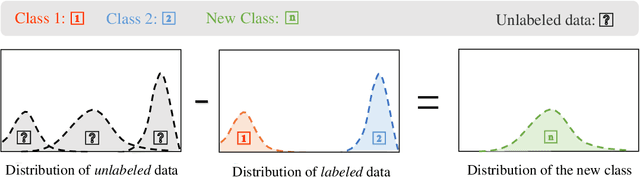
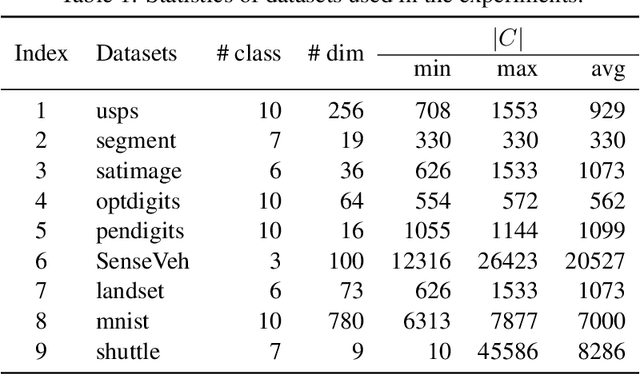
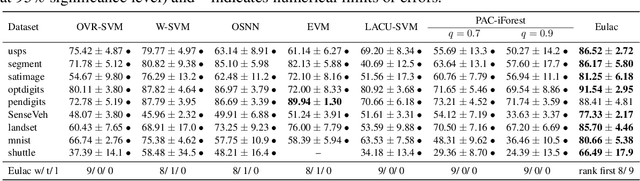
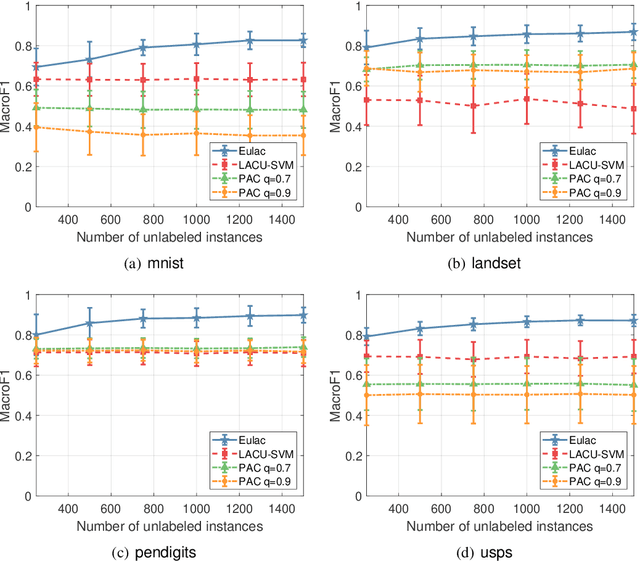
In this paper, we study the problem of learning with augmented classes (LAC), where new classes that do not appear in the training dataset might emerge in the testing phase. The mixture of known classes and new classes in the testing distribution makes the LAC problem quite challenging. Our discovery is that by exploiting cheap and vast unlabeled data, the testing distribution can be estimated in the training stage, which paves us a way to develop algorithms with nice statistical properties. Specifically, we propose an unbiased risk estimator over the testing distribution for the LAC problem, and further develop an efficient algorithm to perform the empirical risk minimization. Both asymptotic and non-asymptotic analyses are provided as theoretical guarantees. The efficacy of the proposed algorithm is also confirmed by experiments.