An SMT Based Compositional Algorithm to Solve a Conflict-Free Electric Vehicle Routing Problem
Paper and Code
Jun 30, 2021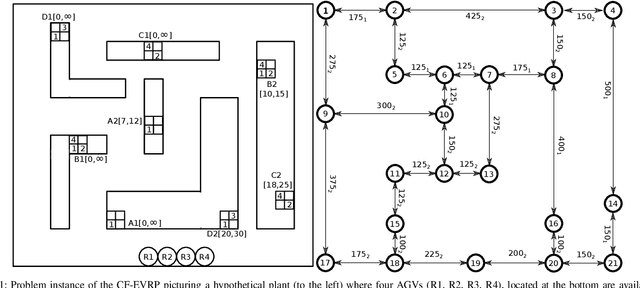
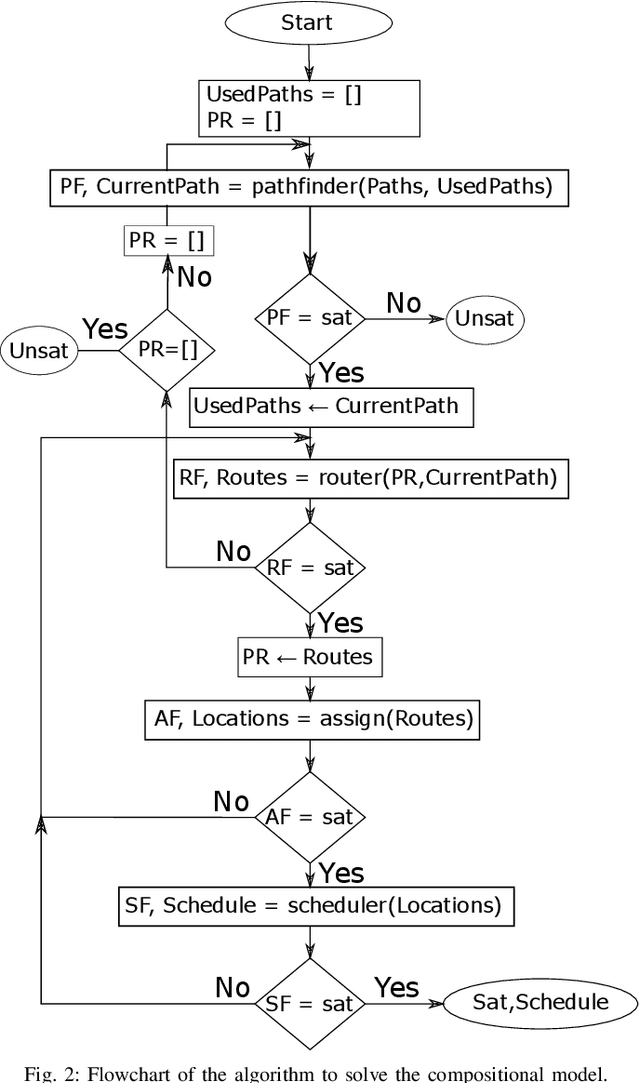
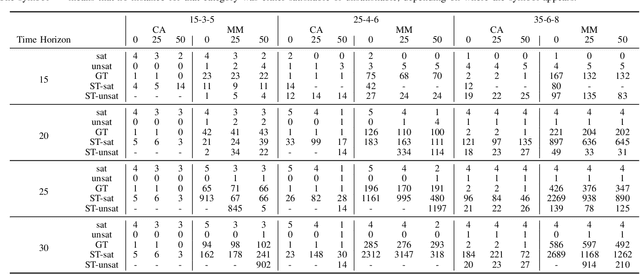
The Vehicle Routing Problem (VRP) is the combinatorial optimization problem of designing routes for vehicles to visit customers in such a fashion that a cost function, typically the number of vehicles, or the total travelled distance is minimized. The problem finds applications in industrial scenarios, for example where Automated Guided Vehicles run through the plant to deliver components from the warehouse. This specific problem, henceforth called the Electric Conflict-Free Vehicle Routing Problem (CF-EVRP), involves constraints such as limited operating range of the vehicles, time windows on the delivery to the customers, and limited capacity on the number of vehicles the road segments can accommodate at the same time. Such a complex system results in a large model that cannot easily be solved to optimality in reasonable time. We therefore developed a compositional model that breaks down the problem into smaller and simpler sub-problems and provides sub-optimal, feasible solutions to the original problem. The algorithm exploits the strengths of SMT solvers, which proved in our previous work to be an efficient approach to deal with scheduling problems. Compared to a monolithic model for the CF-EVRP, written in the SMT standard language and solved using a state-of-the-art SMT solver the compositional model was found to be significantly faster.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge