An MRP Formulation for Supervised Learning: Generalized Temporal Difference Learning Models
Paper and Code
Apr 23, 2024
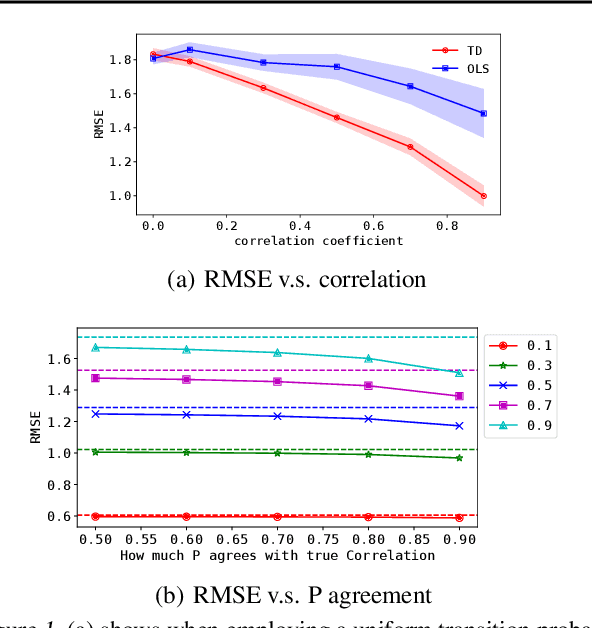
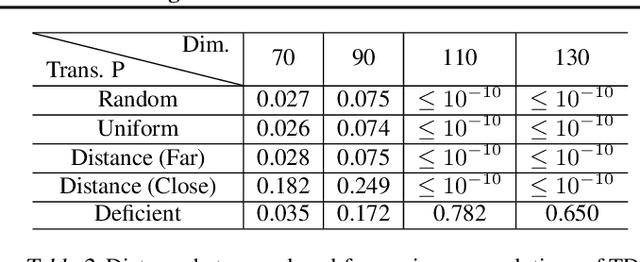
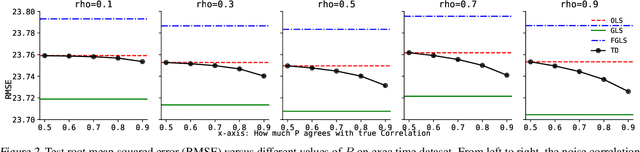
In traditional statistical learning, data points are usually assumed to be independently and identically distributed (i.i.d.) following an unknown probability distribution. This paper presents a contrasting viewpoint, perceiving data points as interconnected and employing a Markov reward process (MRP) for data modeling. We reformulate the typical supervised learning as an on-policy policy evaluation problem within reinforcement learning (RL), introducing a generalized temporal difference (TD) learning algorithm as a resolution. Theoretically, our analysis draws connections between the solutions of linear TD learning and ordinary least squares (OLS). We also show that under specific conditions, particularly when noises are correlated, the TD's solution proves to be a more effective estimator than OLS. Furthermore, we establish the convergence of our generalized TD algorithms under linear function approximation. Empirical studies verify our theoretical results, examine the vital design of our TD algorithm and show practical utility across various datasets, encompassing tasks such as regression and image classification with deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge