An Investigation into Neural Net Optimization via Hessian Eigenvalue Density
Paper and Code
Jan 29, 2019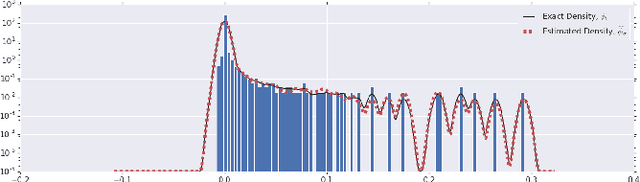
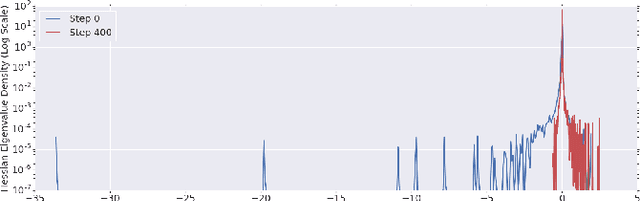
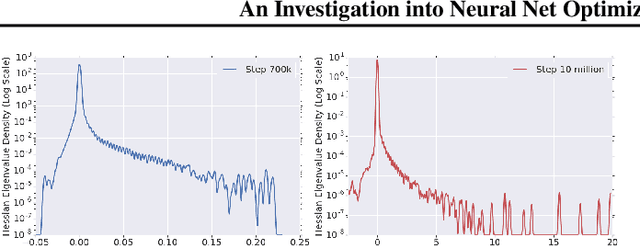
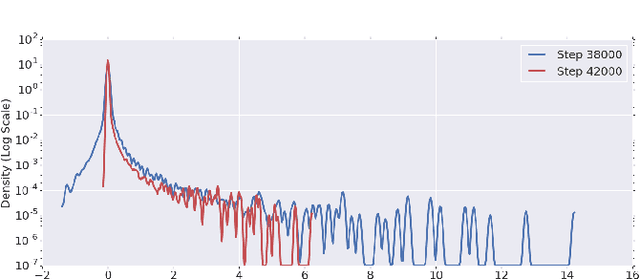
To understand the dynamics of optimization in deep neural networks, we develop a tool to study the evolution of the entire Hessian spectrum throughout the optimization process. Using this, we study a number of hypotheses concerning smoothness, curvature, and sharpness in the deep learning literature. We then thoroughly analyze a crucial structural feature of the spectra: in non-batch normalized networks, we observe the rapid appearance of large isolated eigenvalues in the spectrum, along with a surprising concentration of the gradient in the corresponding eigenspaces. In batch normalized networks, these two effects are almost absent. We characterize these effects, and explain how they affect optimization speed through both theory and experiments. As part of this work, we adapt advanced tools from numerical linear algebra that allow scalable and accurate estimation of the entire Hessian spectrum of ImageNet-scale neural networks; this technique may be of independent interest in other applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge