An Information-Theoretic Approach for Automatically Determining the Number of States when Aggregating Markov Chains
Paper and Code
Jul 05, 2021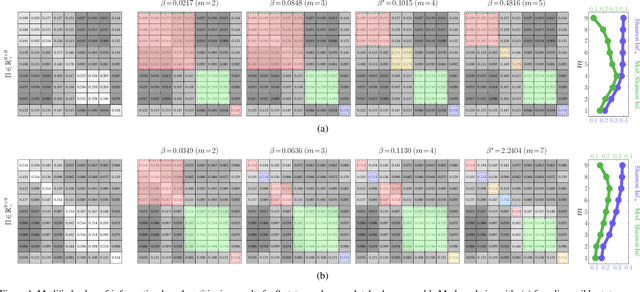
A fundamental problem when aggregating Markov chains is the specification of the number of state groups. Too few state groups may fail to sufficiently capture the pertinent dynamics of the original, high-order Markov chain. Too many state groups may lead to a non-parsimonious, reduced-order Markov chain whose complexity rivals that of the original. In this paper, we show that an augmented value-of-information-based approach to aggregating Markov chains facilitates the determination of the number of state groups. The optimal state-group count coincides with the case where the complexity of the reduced-order chain is balanced against the mutual dependence between the original- and reduced-order chain dynamics.
* Submitted to IEEE ICASSP. arXiv admin note: substantial text overlap
with arXiv:1903.09266
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge