An Improved Training Procedure for Neural Autoregressive Data Completion
Paper and Code
Nov 23, 2017
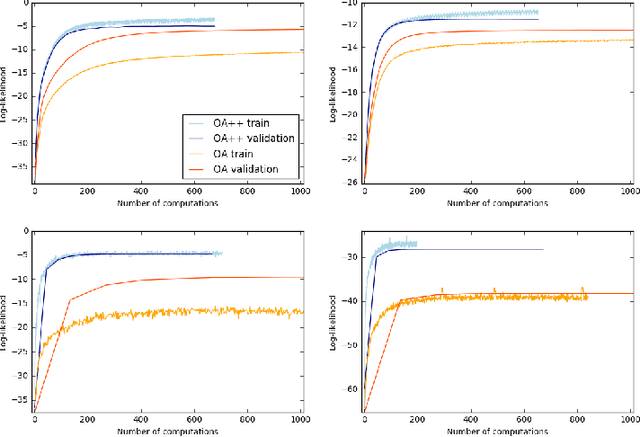
Neural autoregressive models are explicit density estimators that achieve state-of-the-art likelihoods for generative modeling. The D-dimensional data distribution is factorized into an autoregressive product of one-dimensional conditional distributions according to the chain rule. Data completion is a more involved task than data generation: the model must infer missing variables for any partially observed input vector. Previous work introduced an order-agnostic training procedure for data completion with autoregressive models. Missing variables in any partially observed input vector can be imputed efficiently by choosing an ordering where observed dimensions precede unobserved ones and by computing the autoregressive product in this order. In this paper, we provide evidence that the order-agnostic (OA) training procedure is suboptimal for data completion. We propose an alternative procedure (OA++) that reaches better performance in fewer computations. It can handle all data completion queries while training fewer one-dimensional conditional distributions than the OA procedure. In addition, these one-dimensional conditional distributions are trained proportionally to their expected usage at inference time, reducing overfitting. Finally, our OA++ procedure can exploit prior knowledge about the distribution of inference completion queries, as opposed to OA. We support these claims with quantitative experiments on standard datasets used to evaluate autoregressive generative models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge