An Extreme Learning Machine-Based Method for Computational PDEs in Higher Dimensions
Paper and Code
Sep 13, 2023

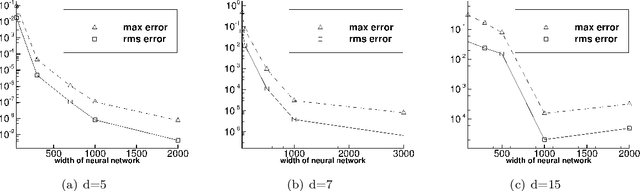
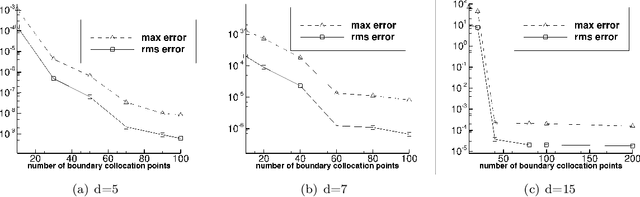
We present two effective methods for solving high-dimensional partial differential equations (PDE) based on randomized neural networks. Motivated by the universal approximation property of this type of networks, both methods extend the extreme learning machine (ELM) approach from low to high dimensions. With the first method the unknown solution field in $d$ dimensions is represented by a randomized feed-forward neural network, in which the hidden-layer parameters are randomly assigned and fixed while the output-layer parameters are trained. The PDE and the boundary/initial conditions, as well as the continuity conditions (for the local variant of the method), are enforced on a set of random interior/boundary collocation points. The resultant linear or nonlinear algebraic system, through its least squares solution, provides the trained values for the network parameters. With the second method the high-dimensional PDE problem is reformulated through a constrained expression based on an Approximate variant of the Theory of Functional Connections (A-TFC), which avoids the exponential growth in the number of terms of TFC as the dimension increases. The free field function in the A-TFC constrained expression is represented by a randomized neural network and is trained by a procedure analogous to the first method. We present ample numerical simulations for a number of high-dimensional linear/nonlinear stationary/dynamic PDEs to demonstrate their performance. These methods can produce accurate solutions to high-dimensional PDEs, in particular with their errors reaching levels not far from the machine accuracy for relatively lower dimensions. Compared with the physics-informed neural network (PINN) method, the current method is both cost-effective and more accurate for high-dimensional PDEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge