An Extended Symbolic-Arithmetic Model for Teaching Double-Black Removal with Rotation in Red-Black Trees

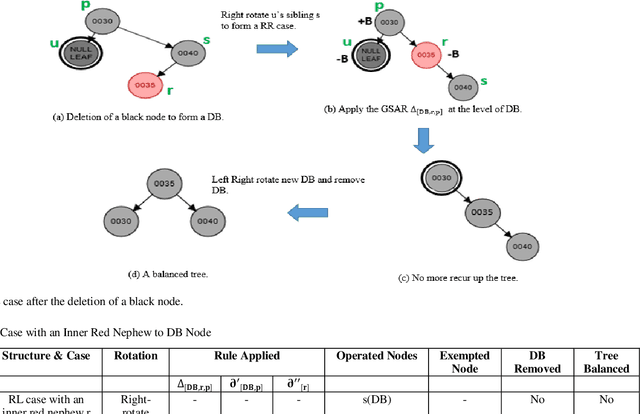
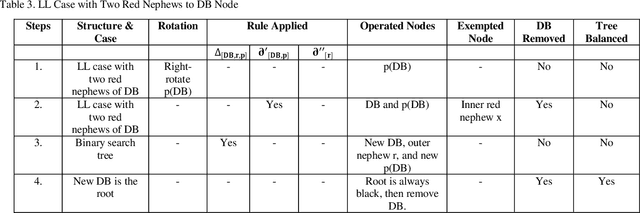
Double-black (DB) nodes have no place in red-black (RB) trees. So when DB nodes are formed, they are immediately removed. The removal of DB nodes that cause rotation and recoloring of other connected nodes poses greater challenges in the teaching and learning of RB trees. To ease this difficulty, this paper extends our previous work on the symbolic arithmetic algebraic (SA) method for removing DB nodes. The SA operations that are given as, Red + Black = Black; Black - Black = Red; Black + Black = DB; and DB - Black = Black removes DB nodes and rebalances black heights in RB trees. By extension, this paper projects three SA mathematical equations, namely, general symbolic arithmetic rule; partial symbolic arithmetic rule1; and partial symbolic arithmetic rule2. The removal of a DB node ultimately affects black heights in RB trees. To balance black heights using the SA equations, all the RB tree cases, namely, LR, RL, LL, and RR, were considered in this work; and the position of the nodes connected directly or indirectly to the DB node was also tested. In this study, to balance a RB tree, the issues considered w.r.t. the different cases of the RB tree were i) whether a DB node has an inner, outer, or both inner and outer black nephews; or ii) whether a DB node has an inner, outer or both inner and outer red nephews. The nephews r and x in this work are the children of the sibling s to a DB, and further up the tree, the parent p of a DB is their grandparent g. Thus, r and x have indirect relationships to a DB at the point of formation of the DB node. The novelty of the SA equations is in their effectiveness in the removal of DB that involves rotation of nodes as well as the recoloring of nodes along any simple path so as to balance black heights in a tree.