An Extended Kuramoto Model for Frequency and Phase Synchronization in Delay-Free Networks with Finite Number of Agents
Paper and Code
Mar 20, 2024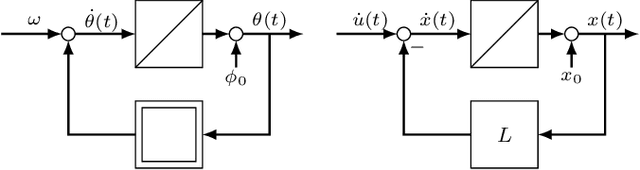
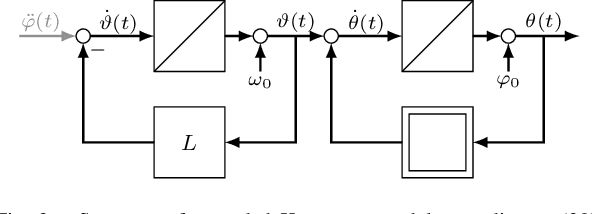
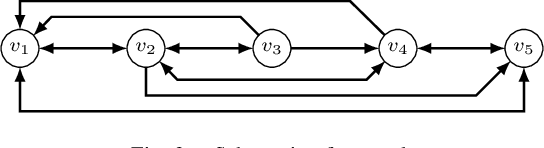
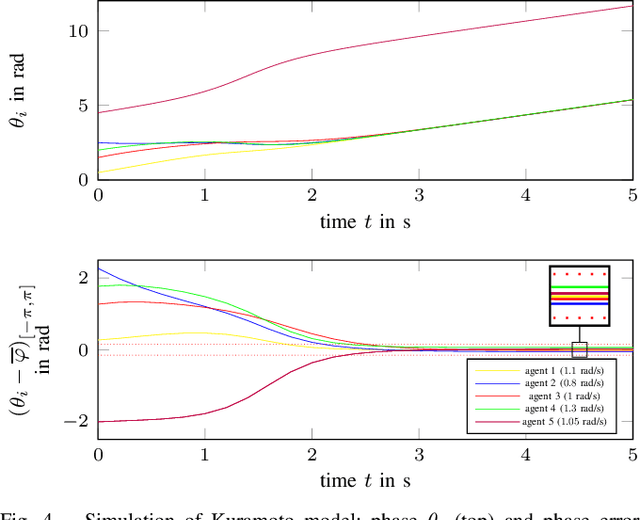
Due to its description of a synchronization between oscillators, the Kuramoto model is an ideal choice for a synchronisation algorithm in networked systems. This requires to achieve not only a frequency synchronization but also a phase synchronization - something the standard Kuramoto model can not provide for a finite number of agents. In this case, a remaining phase difference is necessary to offset differences of the natural frequencies. Setting the Kuramoto model into the context of dynamic consensus and making use of the $n$th order discrete average consensus algorithm, this paper extends the standard Kuramoto model in such a way that frequency and phase synchronization are separated. This in turn leads to an algorithm achieve the required frequency and phase synchronization also for a finite number of agents. Simulations show the viability of this extended Kuramoto model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge