An Experimental Design Approach for Regret Minimization in Logistic Bandits
Paper and Code
Feb 04, 2022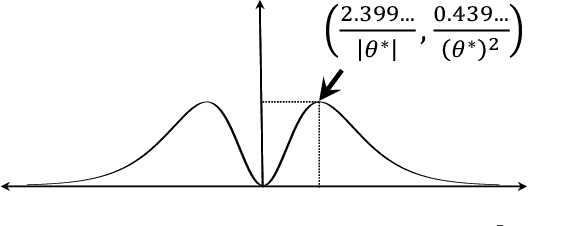

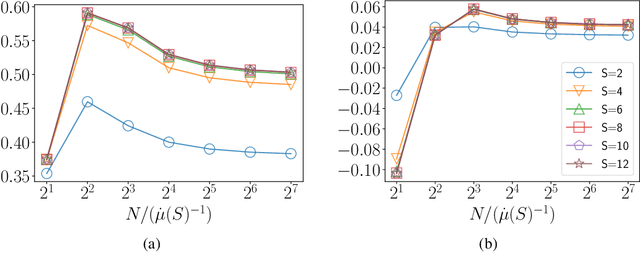
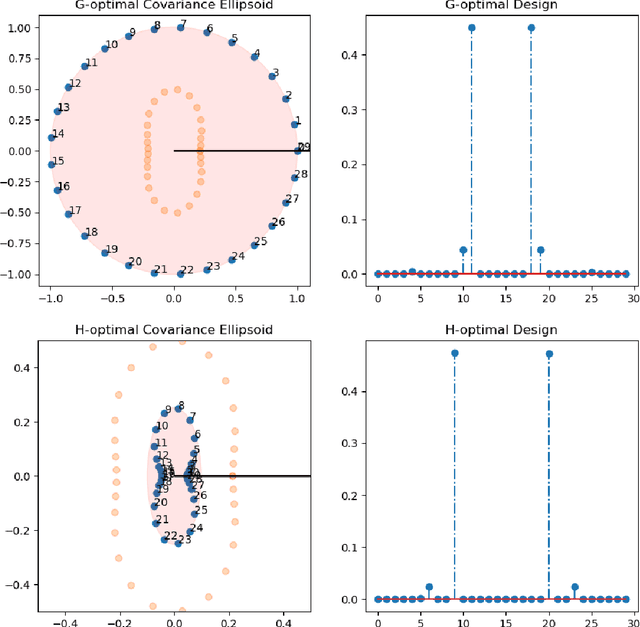
In this work we consider the problem of regret minimization for logistic bandits. The main challenge of logistic bandits is reducing the dependence on a potentially large problem dependent constant $\kappa$ that can at worst scale exponentially with the norm of the unknown parameter $\theta_{\ast}$. Abeille et al. (2021) have applied self-concordance of the logistic function to remove this worst-case dependence providing regret guarantees like $O(d\log^2(\kappa)\sqrt{\dot\mu T}\log(|\mathcal{X}|))$ where $d$ is the dimensionality, $T$ is the time horizon, and $\dot\mu$ is the variance of the best-arm. This work improves upon this bound in the fixed arm setting by employing an experimental design procedure that achieves a minimax regret of $O(\sqrt{d \dot\mu T\log(|\mathcal{X}|)})$. Our regret bound in fact takes a tighter instance (i.e., gap) dependent regret bound for the first time in logistic bandits. We also propose a new warmup sampling algorithm that can dramatically reduce the lower order term in the regret in general and prove that it can replace the lower order term dependency on $\kappa$ to $\log^2(\kappa)$ for some instances. Finally, we discuss the impact of the bias of the MLE on the logistic bandit problem, providing an example where $d^2$ lower order regret (cf., it is $d$ for linear bandits) may not be improved as long as the MLE is used and how bias-corrected estimators may be used to make it closer to $d$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge