An Evolutionary Stochastic-Local-Search Framework for One-Dimensional Cutting-Stock Problems
Paper and Code
Jul 27, 2017

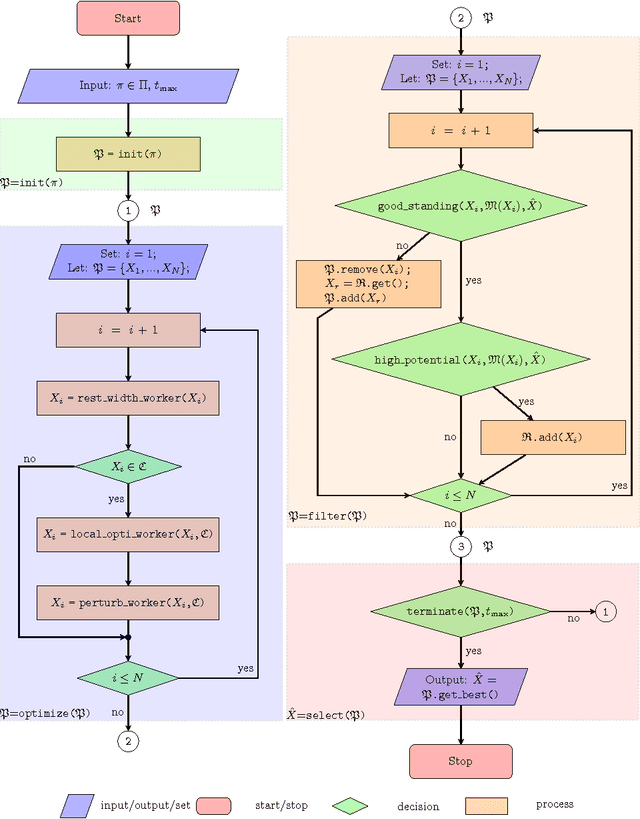

We introduce an evolutionary stochastic-local-search (SLS) algorithm for addressing a generalized version of the so-called 1/V/D/R cutting-stock problem. Cutting-stock problems are encountered often in industrial environments and the ability to address them efficiently usually results in large economic benefits. Traditionally linear-programming-based techniques have been utilized to address such problems, however their flexibility might be limited when nonlinear constraints and objective functions are introduced. To this end, this paper proposes an evolutionary SLS algorithm for addressing one-dimensional cutting-stock problems. The contribution lies in the introduction of a flexible structural framework of the optimization that may accommodate a large family of diversification strategies including a novel parallel pattern appropriate for SLS algorithms (not necessarily restricted to cutting-stock problems). We finally demonstrate through experiments in a real-world manufacturing problem the benefit in cost reduction of the considered diversification strategies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge