An Entropic Associative Memory
Paper and Code
Sep 28, 2020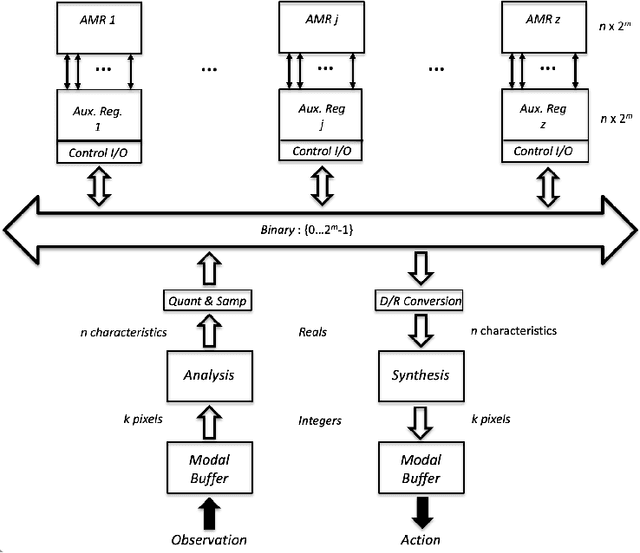



Natural memories are associative, declarative and distributed. Symbolic computing memories resemble natural memories in their declarative character, and information can be stored and recovered explicitly; however, they lack the associative and distributed properties of natural memories. Sub-symbolic memories developed within the connectionist or artificial neural networks paradigm are associative and distributed, but are unable to express symbolic structure and information cannot be stored and retrieved explicitly; hence, they lack the declarative property. To address this dilemma, we use Relational-Indeterminate Computing to model associative memory registers that hold distributed representations of individual objects. This mode of computing has an intrinsic computing entropy which measures the indeterminacy of representations. This parameter determines the operational characteristics of the memory. Associative registers are embedded in an architecture that maps concrete images expressed in modality-specific buffers into abstract representations, and vice versa, and the memory system as a whole fulfills the three properties of natural memories. The system has been used to model a visual memory holding the representations of hand-written digits, and recognition and recall experiments show that there is a range of entropy values, not too low and not too high, in which associative memory registers have a satisfactory performance. The similarity between the cue and the object recovered in memory retrieve operations depends on the entropy of the memory register holding the representation of the corresponding object. The experiments were implemented in a simulation using a standard computer, but a parallel architecture may be built where the memory operations would take a very reduced number of computing steps.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge