An Empirically Grounded Identifiability Theory Will Accelerate Self-Supervised Learning Research

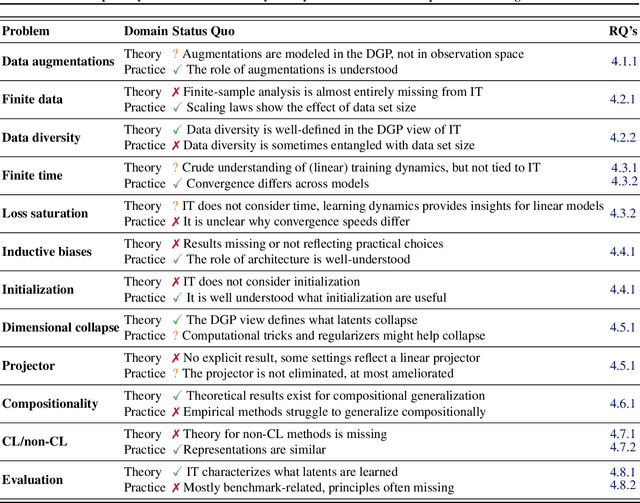
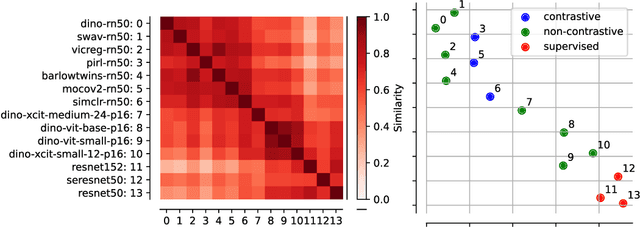
Self-Supervised Learning (SSL) powers many current AI systems. As research interest and investment grow, the SSL design space continues to expand. The Platonic view of SSL, following the Platonic Representation Hypothesis (PRH), suggests that despite different methods and engineering approaches, all representations converge to the same Platonic ideal. However, this phenomenon lacks precise theoretical explanation. By synthesizing evidence from Identifiability Theory (IT), we show that the PRH can emerge in SSL. However, current IT cannot explain SSL's empirical success. To bridge the gap between theory and practice, we propose expanding IT into what we term Singular Identifiability Theory (SITh), a broader theoretical framework encompassing the entire SSL pipeline. SITh would allow deeper insights into the implicit data assumptions in SSL and advance the field towards learning more interpretable and generalizable representations. We highlight three critical directions for future research: 1) training dynamics and convergence properties of SSL; 2) the impact of finite samples, batch size, and data diversity; and 3) the role of inductive biases in architecture, augmentations, initialization schemes, and optimizers.