An Empirical Comparison of Off-policy Prediction Learning Algorithms in the Four Rooms Environment

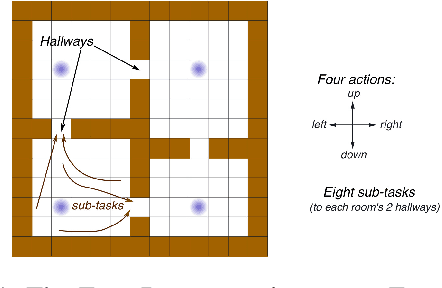
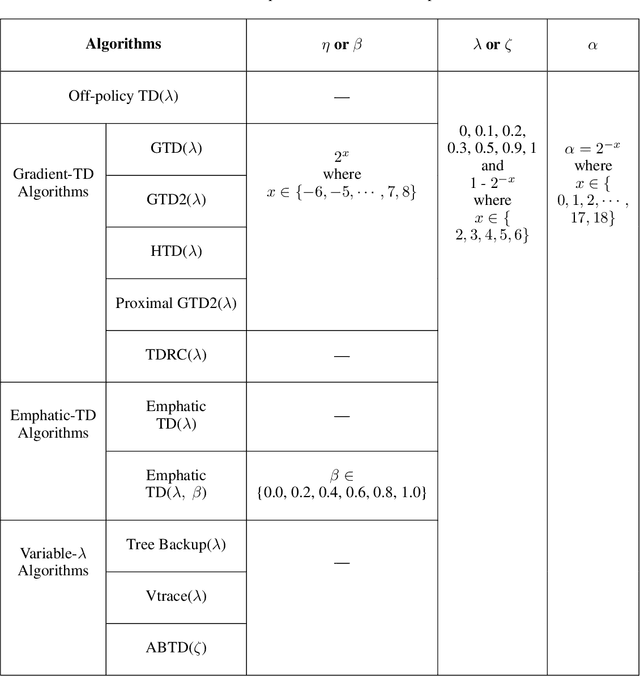
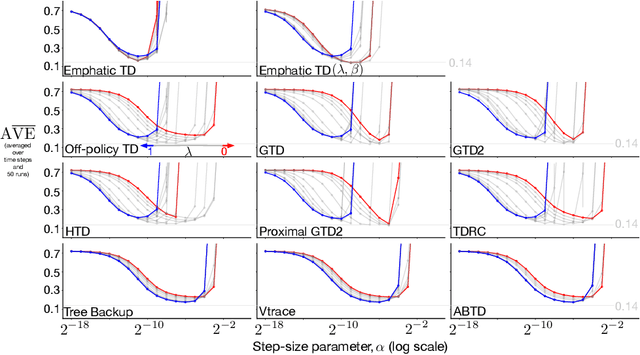
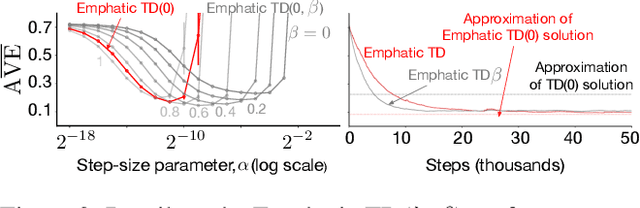
Many off-policy prediction learning algorithms have been proposed in the past decade, but it remains unclear which algorithms learn faster than others. We empirically compare 11 off-policy prediction learning algorithms with linear function approximation on two small tasks: the Rooms task, and the High Variance Rooms task. The tasks are designed such that learning fast in them is challenging. In the Rooms task, the product of importance sampling ratios can be as large as $2^{14}$ and can sometimes be two. To control the high variance caused by the product of the importance sampling ratios, step size should be set small, which in turn slows down learning. The High Variance Rooms task is more extreme in that the product of the ratios can become as large as $2^{14}\times 25$. This paper builds upon the empirical study of off-policy prediction learning algorithms by Ghiassian and Sutton (2021). We consider the same set of algorithms as theirs and employ the same experimental methodology. The algorithms considered are: Off-policy TD($\lambda$), five Gradient-TD algorithms, two Emphatic-TD algorithms, Tree Backup($\lambda$), Vtrace($\lambda$), and ABTD($\zeta$). We found that the algorithms' performance is highly affected by the variance induced by the importance sampling ratios. The data shows that Tree Backup($\lambda$), Vtrace($\lambda$), and ABTD($\zeta$) are not affected by the high variance as much as other algorithms but they restrict the effective bootstrapping parameter in a way that is too limiting for tasks where high variance is not present. We observed that Emphatic TD($\lambda$) tends to have lower asymptotic error than other algorithms, but might learn more slowly in some cases. We suggest algorithms for practitioners based on their problem of interest, and suggest approaches that can be applied to specific algorithms that might result in substantially improved algorithms.