An Efficient Protocol for Negotiation over Combinatorial Domains with Incomplete Information
Paper and Code
Feb 14, 2012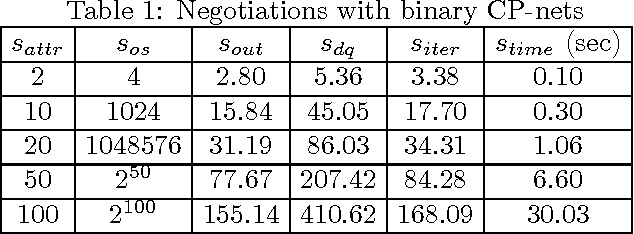
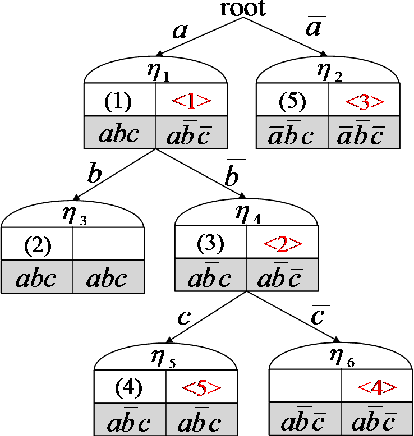
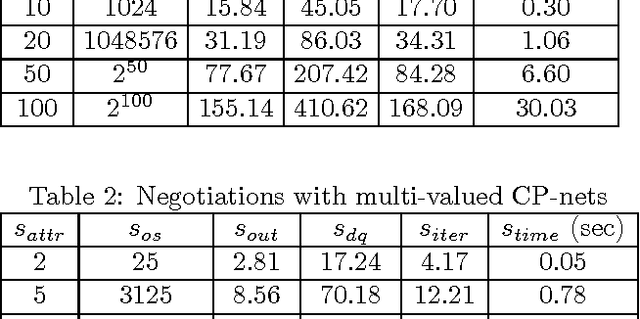

We study the problem of agent-based negotiation in combinatorial domains. It is difficult to reach optimal agreements in bilateral or multi-lateral negotiations when the agents' preferences for the possible alternatives are not common knowledge. Self-interested agents often end up negotiating inefficient agreements in such situations. In this paper, we present a protocol for negotiation in combinatorial domains which can lead rational agents to reach optimal agreements under incomplete information setting. Our proposed protocol enables the negotiating agents to identify efficient solutions using distributed search that visits only a small subspace of the whole outcome space. Moreover, the proposed protocol is sufficiently general that it is applicable to most preference representation models in combinatorial domains. We also present results of experiments that demonstrate the feasibility and computational efficiency of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge