An Adaptive Memory Multi-Batch L-BFGS Algorithm for Neural Network Training
Paper and Code
Dec 14, 2020


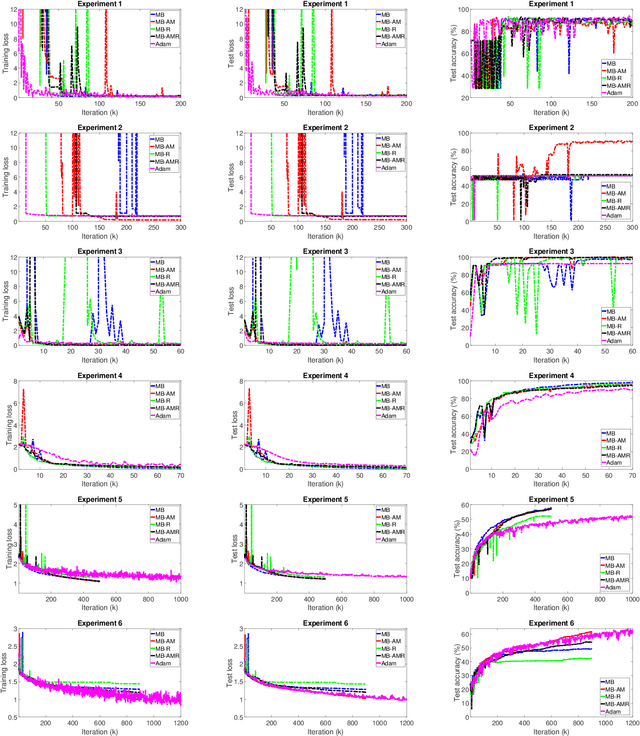
Motivated by the potential for parallel implementation of batch-based algorithms and the accelerated convergence achievable with approximated second order information a limited memory version of the BFGS algorithm has been receiving increasing attention in recent years for large neural network training problems. As the shape of the cost function is generally not quadratic and only becomes approximately quadratic in the vicinity of a minimum, the use of second order information by L-BFGS can be unreliable during the initial phase of training, i.e. when far from a minimum. Therefore, to control the influence of second order information as training progresses, we propose a multi-batch L-BFGS algorithm, namely MB-AM, that gradually increases its trust in the curvature information by implementing a progressive storage and use of curvature data through a development-based increase (dev-increase) scheme. Using six discriminative modelling benchmark problems we show empirically that MB-AM has slightly faster convergence and, on average, achieves better solutions than the standard multi-batch L-BFGS algorithm when training MLP and CNN models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge