Amortized Posterior Sampling with Diffusion Prior Distillation
Paper and Code
Jul 25, 2024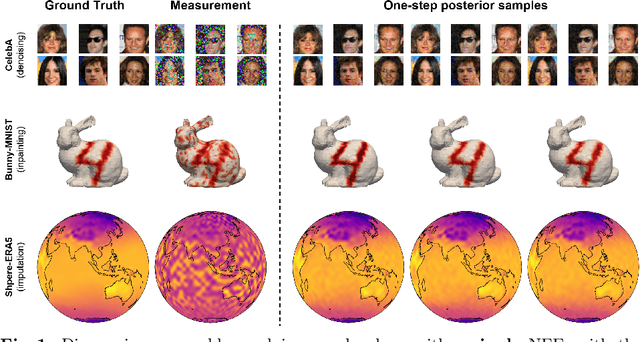

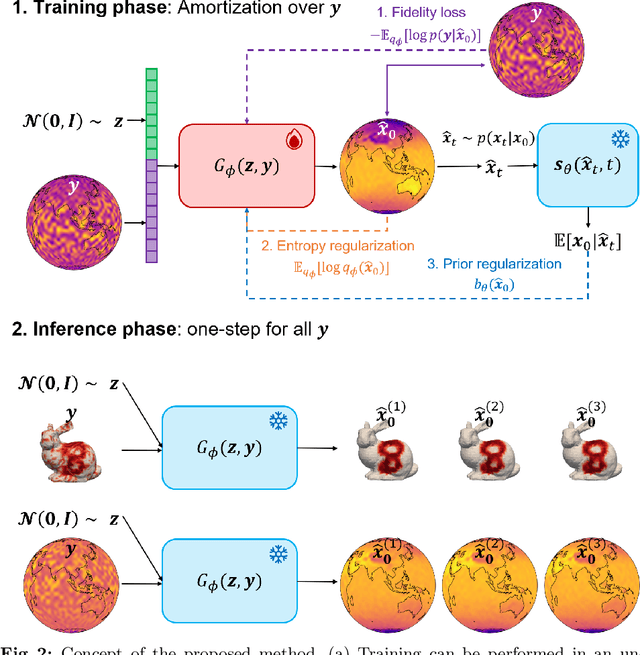

We propose a variational inference approach to sample from the posterior distribution for solving inverse problems. From a pre-trained diffusion model, our approach trains a conditional flow model to minimize the divergence between the proposal variational distribution and the posterior distribution implicitly defined through the diffusion model. Once trained, the flow model is capable of sampling from the posterior distribution with a single NFE, amortized with respect to the measurement. The proposed method paves a new path for distilling a diffusion prior for efficient posterior sampling. We show that our method is applicable to standard signals in Euclidean space, as well as signals on manifold.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge