Almost-Exact Matching with Replacement for Causal Inference

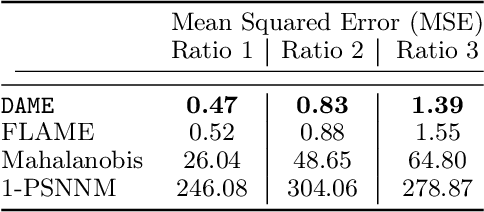
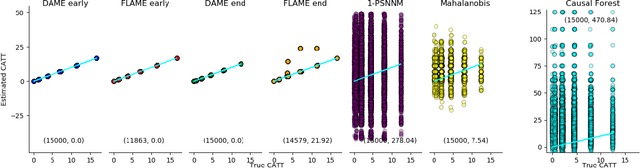
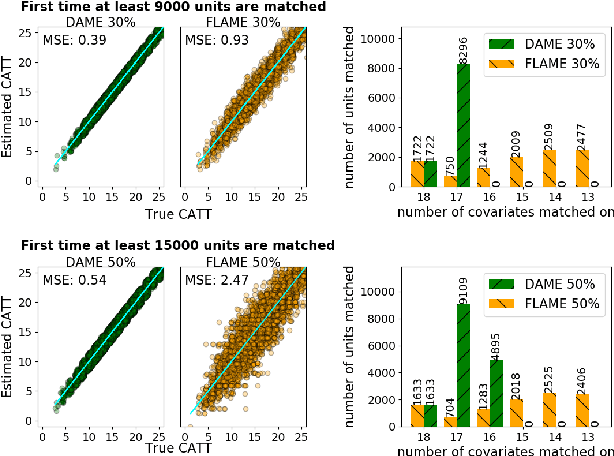
We aim to create the highest possible quality of treatment-control matches for categorical data in the potential outcomes framework. Matching methods are heavily used in the social sciences due to their interpretability, but most matching methods do not pass basic sanity checks: they fail when irrelevant variables are introduced, and tend to be either computationally slow or produce low-quality matches. The method proposed in this work aims to match units on a weighted Hamming distance, taking into account the relative importance of the covariates; the algorithm aims to match units on as many relevant variables as possible. To do this, the algorithm creates a hierarchy of covariate combinations on which to match (similar to downward closure), in the process solving an optimization problem for each unit in order to construct the optimal matches. The algorithm uses a single dynamic program to solve all of the optimization problems simultaneously. Notable advantages of our method over existing matching procedures are its high-quality matches, versatility in handling different data distributions that may have irrelevant variables, and ability to handle missing data by matching on as many available covariates as possible.