Algorithmic Information Design in Multi-Player Games: Possibility and Limits in Singleton Congestion
Paper and Code
Sep 25, 2021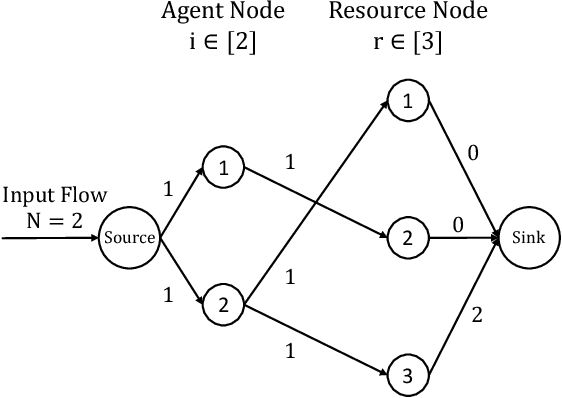


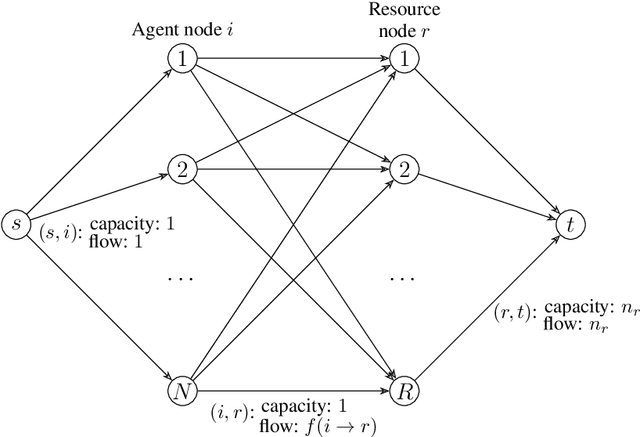
Most algorithmic studies on multi-agent information design so far have focused on the restricted situation with no inter-agent externalities; a few exceptions investigated special game classes such as zero-sum games and second-price auctions but have all focused only on optimal public signaling and exhibit sweepingly negative results. This paper initiates the algorithmic information design of both \emph{public} and \emph{private} signaling in a fundamental class of games with negative externalities, i.e., atomic singleton congestion games, with wide application in today's digital economy, machine scheduling, routing, etc. For both public and private signaling, we show that the optimal information design can be efficiently computed when the number of resources is a constant. To our knowledge, this is the first set of computationally efficient algorithms for information design in succinctly representable many-player games. Our results hinge on novel techniques such as developing ``reduced forms'' to compactly represent players' marginal beliefs. When there are many resources, we show computational intractability results. To overcome the challenge of multiple equilibria, here we introduce a new notion of equilibrium-\emph{oblivious} NP-hardness, which rules out any possibility of computing a good signaling scheme, irrespective of the equilibrium selection rule.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge