Agnostic Physics-Driven Deep Learning
Paper and Code
May 30, 2022
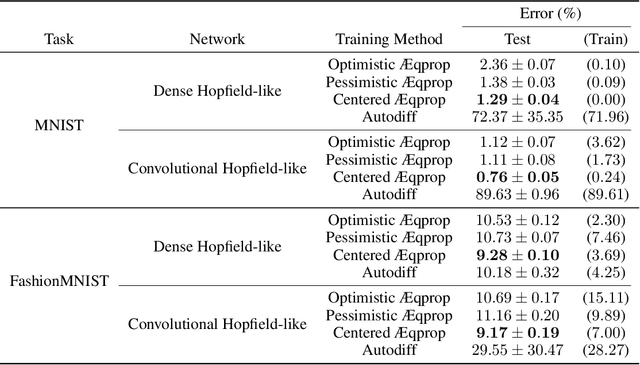
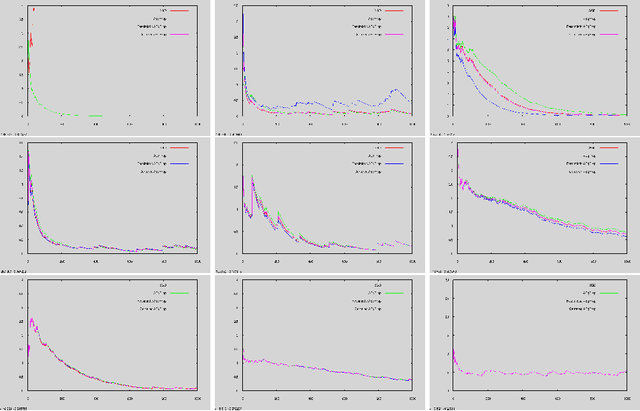

This work establishes that a physical system can perform statistical learning without gradient computations, via an Agnostic Equilibrium Propagation (Aeqprop) procedure that combines energy minimization, homeostatic control, and nudging towards the correct response. In Aeqprop, the specifics of the system do not have to be known: the procedure is based only on external manipulations, and produces a stochastic gradient descent without explicit gradient computations. Thanks to nudging, the system performs a true, order-one gradient step for each training sample, in contrast with order-zero methods like reinforcement or evolutionary strategies, which rely on trial and error. This procedure considerably widens the range of potential hardware for statistical learning to any system with enough controllable parameters, even if the details of the system are poorly known. Aeqprop also establishes that in natural (bio)physical systems, genuine gradient-based statistical learning may result from generic, relatively simple mechanisms, without backpropagation and its requirement for analytic knowledge of partial derivatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge