Adversarial Vulnerability of Neural Networks Increases With Input Dimension

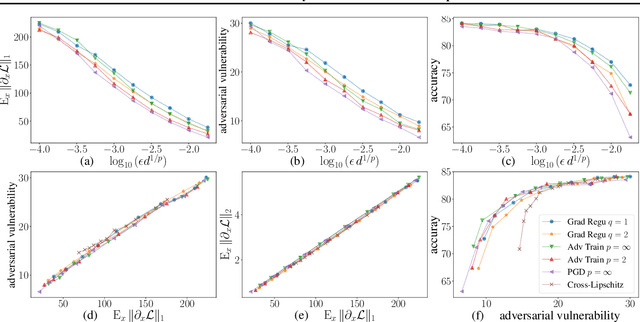
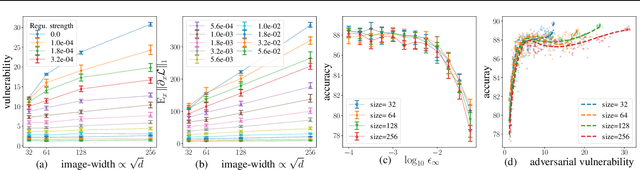
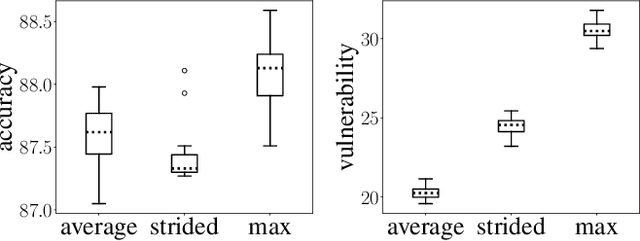
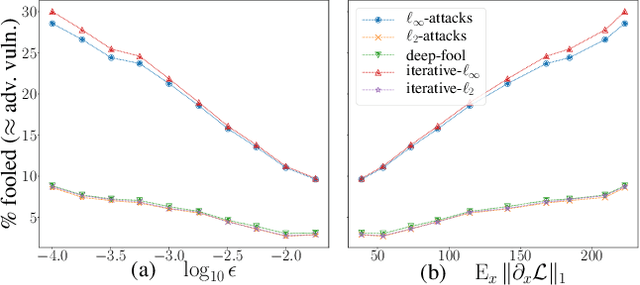
Over the past four years, neural networks have been proven vulnerable to adversarial images: targeted but imperceptible image perturbations lead to drastically different predictions. We show that adversarial vulnerability increases with the gradients of the training objective when viewed as a function of the inputs. For most current network architectures, we prove that the $\ell_1$-norm of these gradients grows as the square root of the input size. These nets therefore become increasingly vulnerable with growing image size. Our proofs rely on the network's weight distribution at initialization, but extensive experiments confirm that our conclusions still hold after training.