Adversarial training may be a double-edged sword
Paper and Code
Jul 24, 2021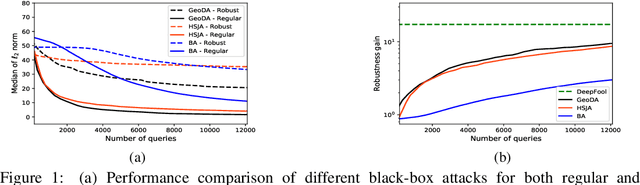

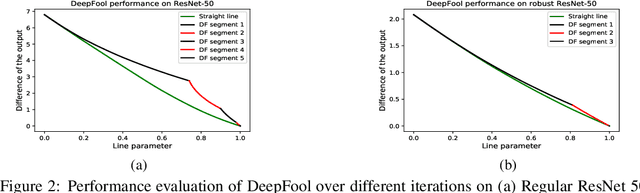
Adversarial training has been shown as an effective approach to improve the robustness of image classifiers against white-box attacks. However, its effectiveness against black-box attacks is more nuanced. In this work, we demonstrate that some geometric consequences of adversarial training on the decision boundary of deep networks give an edge to certain types of black-box attacks. In particular, we define a metric called robustness gain to show that while adversarial training is an effective method to dramatically improve the robustness in white-box scenarios, it may not provide such a good robustness gain against the more realistic decision-based black-box attacks. Moreover, we show that even the minimal perturbation white-box attacks can converge faster against adversarially-trained neural networks compared to the regular ones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge