Adversarial robustness via stochastic regularization of neural activation sensitivity
Paper and Code
Sep 23, 2020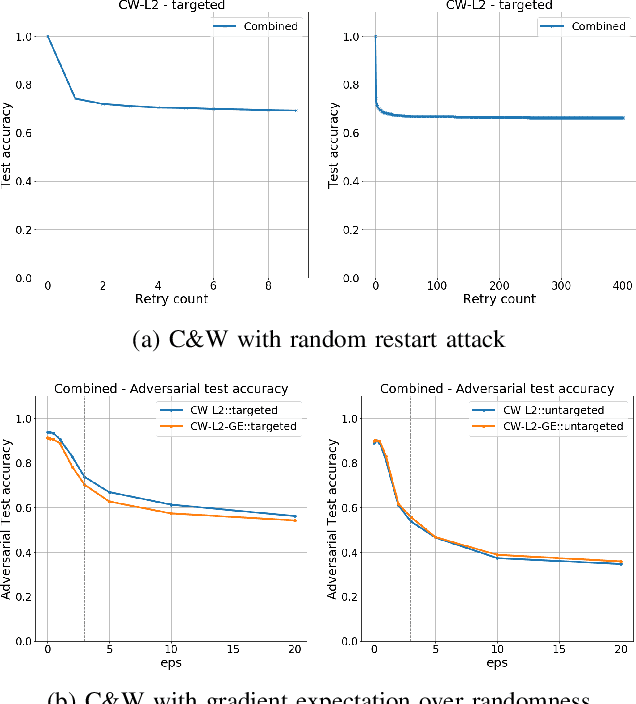
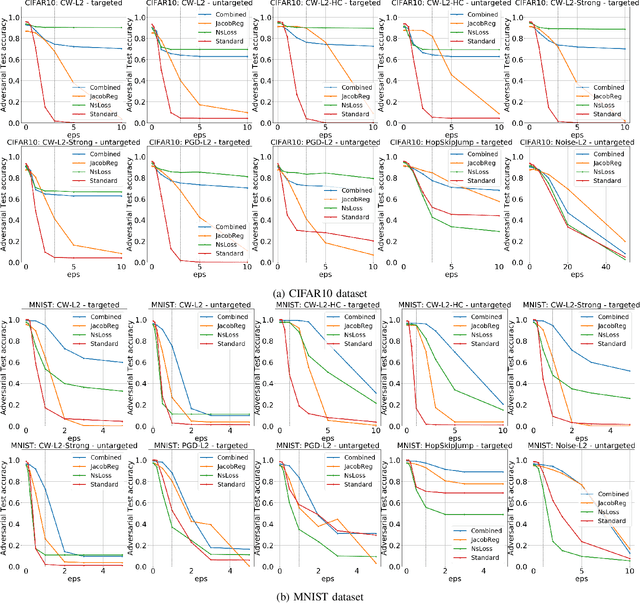
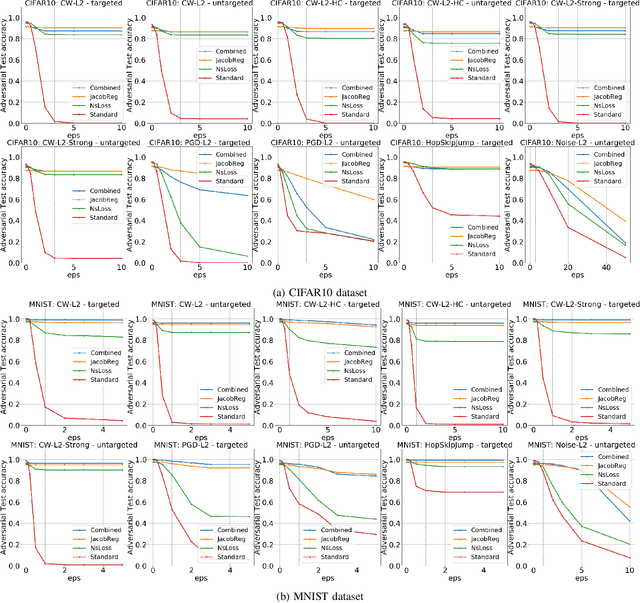
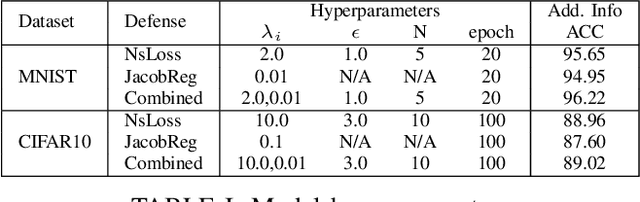
Recent works have shown that the input domain of any machine learning classifier is bound to contain adversarial examples. Thus we can no longer hope to immune classifiers against adversarial examples and instead can only aim to achieve the following two defense goals: 1) making adversarial examples harder to find, or 2) weakening their adversarial nature by pushing them further away from correctly classified data points. Most if not all the previously suggested defense mechanisms attend to just one of those two goals, and as such, could be bypassed by adaptive attacks that take the defense mechanism into consideration. In this work we suggest a novel defense mechanism that simultaneously addresses both defense goals: We flatten the gradients of the loss surface, making adversarial examples harder to find, using a novel stochastic regularization term that explicitly decreases the sensitivity of individual neurons to small input perturbations. In addition, we push the decision boundary away from correctly classified inputs by leveraging Jacobian regularization. We present a solid theoretical basis and an empirical testing of our suggested approach, demonstrate its superiority over previously suggested defense mechanisms, and show that it is effective against a wide range of adaptive attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge