Adversarial Online Learning with Variable Plays in the Pursuit-Evasion Game: Theoretical Foundations and Application in Connected and Automated Vehicle Cybersecurity
Paper and Code
Oct 26, 2021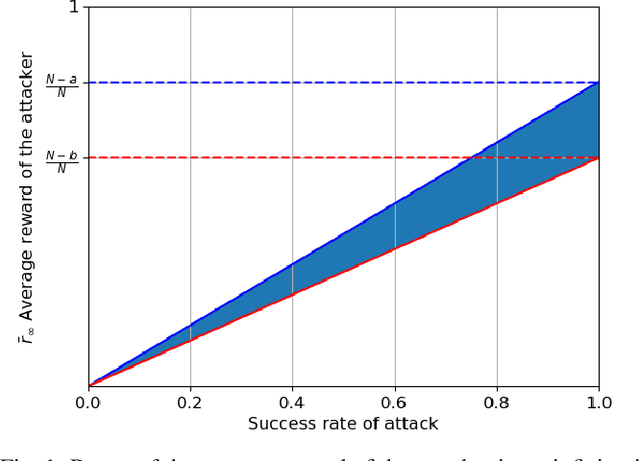
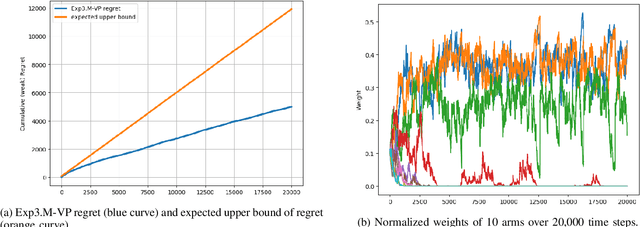
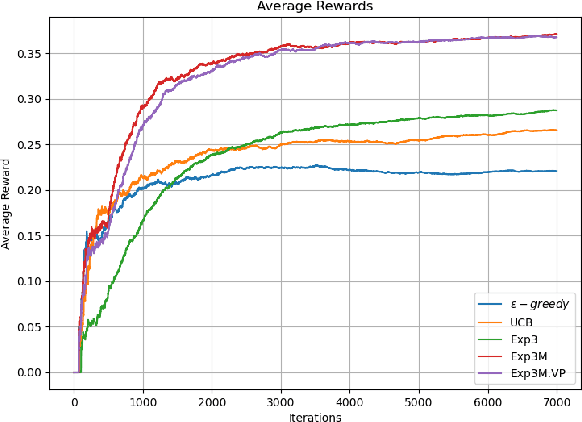
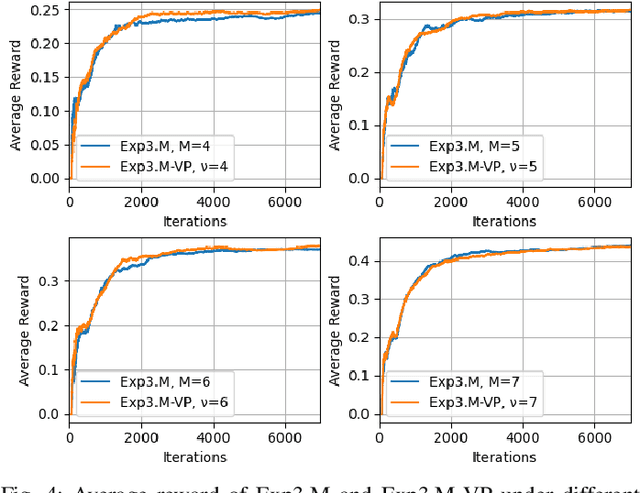
We extend the adversarial/non-stochastic multi-play multi-armed bandit (MPMAB) to the case where the number of arms to play is variable. The work is motivated by the fact that the resources allocated to scan different critical locations in an interconnected transportation system change dynamically over time and depending on the environment. By modeling the malicious hacker and the intrusion monitoring system as the attacker and the defender, respectively, we formulate the problem for the two players as a sequential pursuit-evasion game. We derive the condition under which a Nash equilibrium of the strategic game exists. For the defender side, we provide an exponential-weighted based algorithm with sublinear pseudo-regret. We further extend our model to heterogeneous rewards for both players, and obtain lower and upper bounds on the average reward for the attacker. We provide numerical experiments to demonstrate the effectiveness of a variable-arm play.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge