Additive Models with Trend Filtering

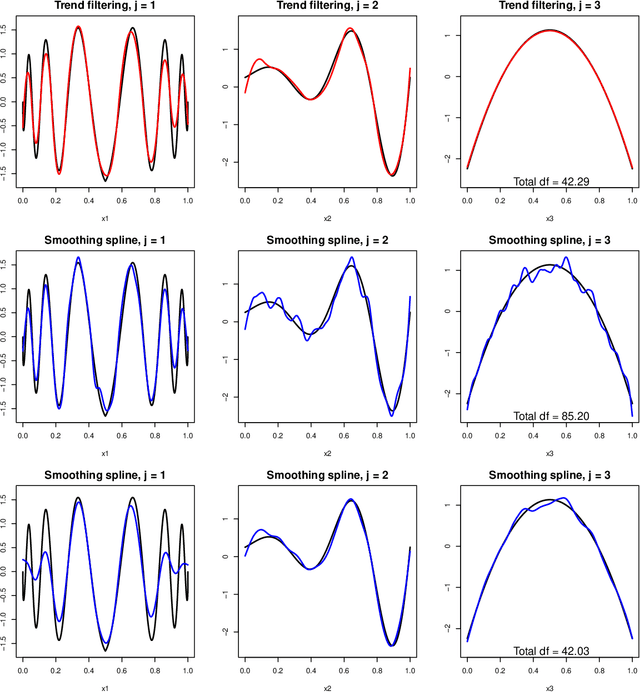
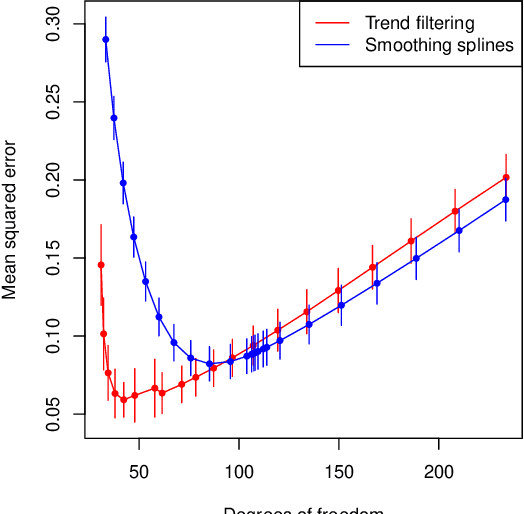
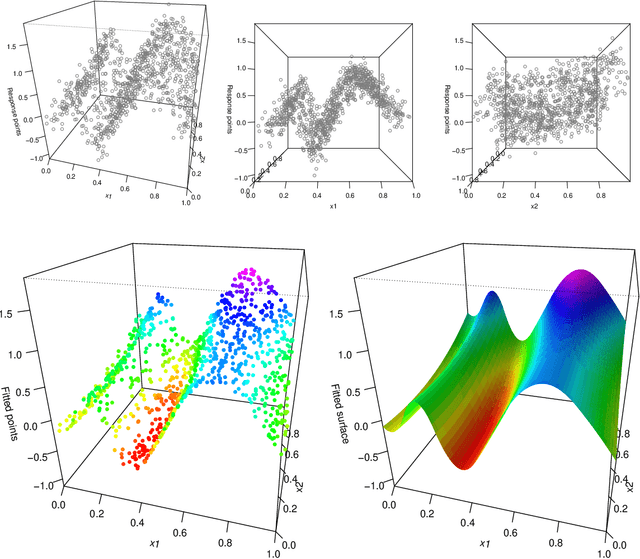
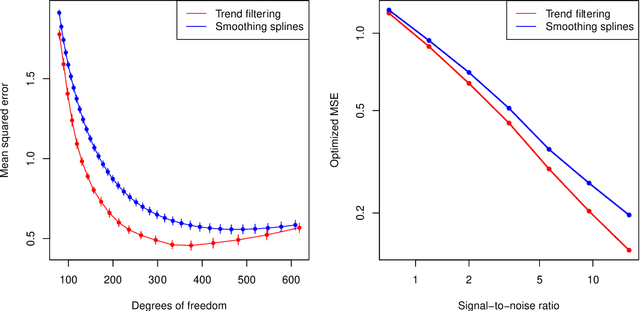
We consider additive models built with trend filtering, i.e., additive models whose components are each regularized by the (discrete) total variation of their $(k+1)$st (discrete) derivative, for a chosen integer $k \geq 0$. This results in $k$th degree piecewise polynomial components, (e.g., $k=0$ gives piecewise constant components, $k=1$ gives piecewise linear, $k=2$ gives piecewise quadratic, etc.). Analogous to its advantages in the univariate case, additive trend filtering has favorable theoretical and computational properties, thanks in large part to the localized nature of the (discrete) total variation regularizer that it uses. On the theory side, we derive fast error rates for additive trend filtering estimates, and show these rates are minimax optimal when the underlying function is additive and has component functions whose derivatives are of bounded variation. We also show that these rates are unattainable by additive smoothing splines (and by additive models built from linear smoothers, in general). On the computational side, as per the standard in additive models, backfitting is an appealing method for optimization, but it is particularly appealing for additive trend filtering because we can leverage a few highly efficient univariate trend filtering solvers. Going one step further, we derive a new backfitting algorithm whose iterations can be run in parallel, which (as far as we know) is the first of its kind. Lastly, we present experiments that examine the empirical performance of additive trend filtering, and outline some possible extensions.