AdaSGD: Bridging the gap between SGD and Adam
Paper and Code
Jun 30, 2020
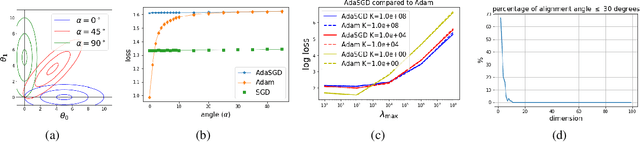
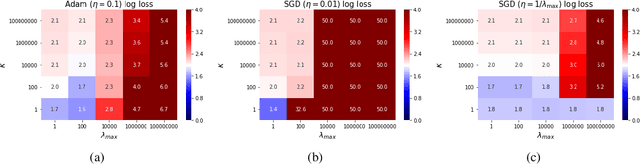
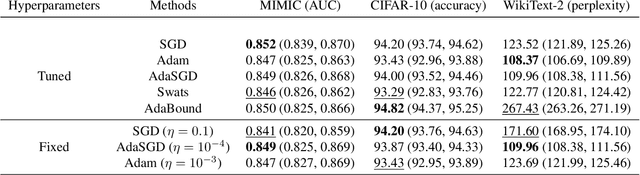
In the context of stochastic gradient descent(SGD) and adaptive moment estimation (Adam),researchers have recently proposed optimization techniques that transition from Adam to SGD with the goal of improving both convergence and generalization performance. However, precisely how each approach trades off early progress and generalization is not well understood; thus, it is unclear when or even if, one should transition from one approach to the other. In this work, by first studying the convex setting, we identify potential contributors to observed differences in performance between SGD and Adam. In particular,we provide theoretical insights for when and why Adam outperforms SGD and vice versa. We ad-dress the performance gap by adapting a single global learning rate for SGD, which we refer to as AdaSGD. We justify this proposed approach with empirical analyses in non-convex settings. On several datasets that span three different domains,we demonstrate how AdaSGD combines the benefits of both SGD and Adam, eliminating the need for approaches that transition from Adam to SGD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge