Adaptively Pruning Features for Boosted Decision Trees
Paper and Code
May 19, 2018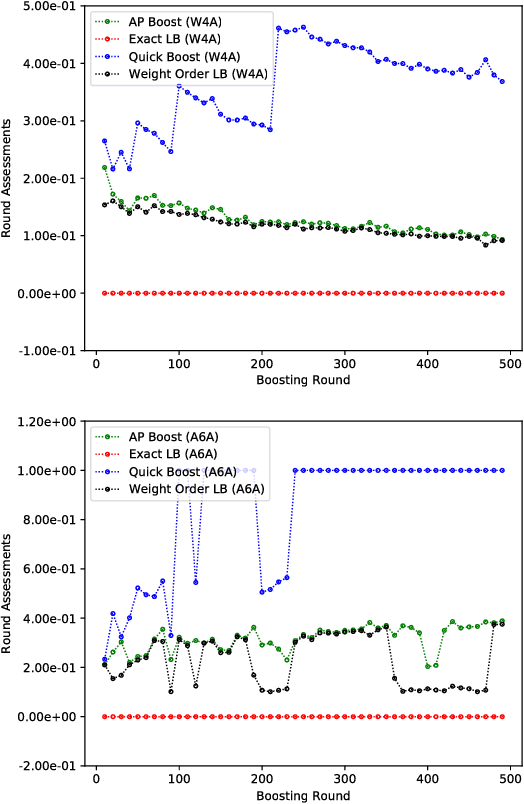

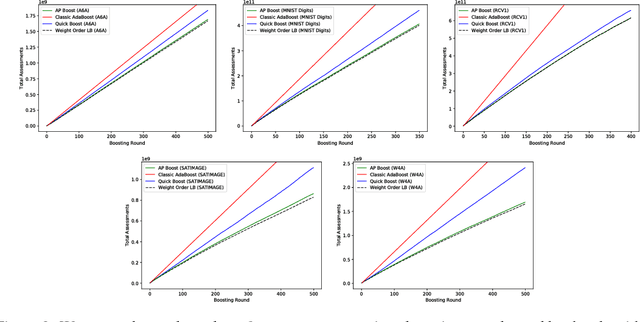

Boosted decision trees enjoy popularity in a variety of applications; however, for large-scale datasets, the cost of training a decision tree in each round can be prohibitively expensive. Inspired by ideas from the multi-arm bandit literature, we develop a highly efficient algorithm for computing exact greedy-optimal decision trees, outperforming the state-of-the-art Quick Boost method. We further develop a framework for deriving lower bounds on the problem that applies to a wide family of conceivable algorithms for the task (including our algorithm and Quick Boost), and we demonstrate empirically on a wide variety of data sets that our algorithm is near-optimal within this family of algorithms. We also derive a lower bound applicable to any algorithm solving the task, and we demonstrate that our algorithm empirically achieves performance close to this best-achievable lower bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge