Adaptive sparseness for correntropy-based robust regression via automatic relevance determination
Paper and Code
Jan 31, 2023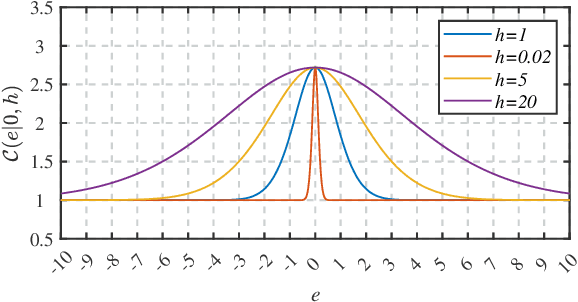
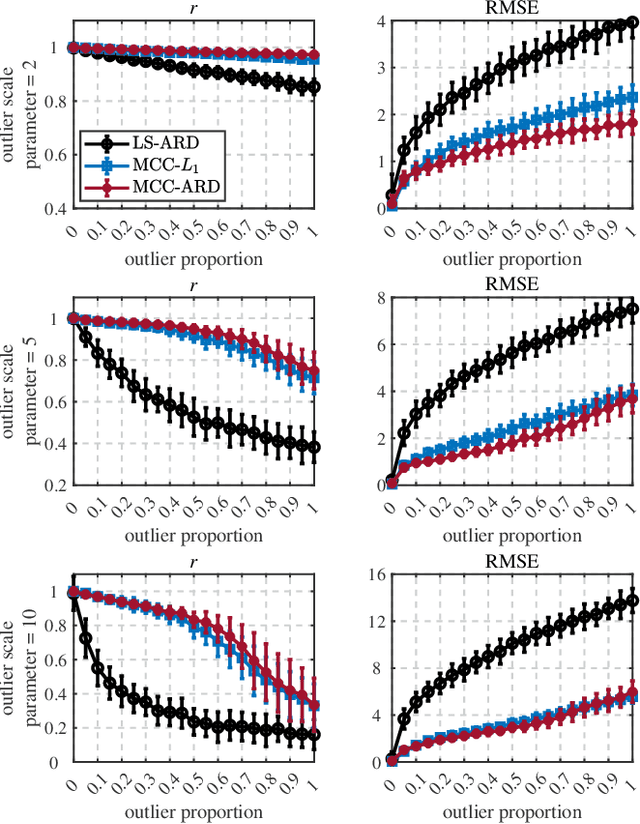
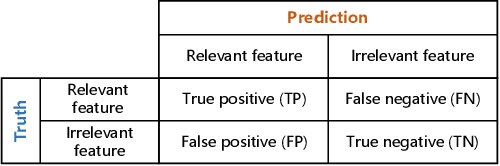
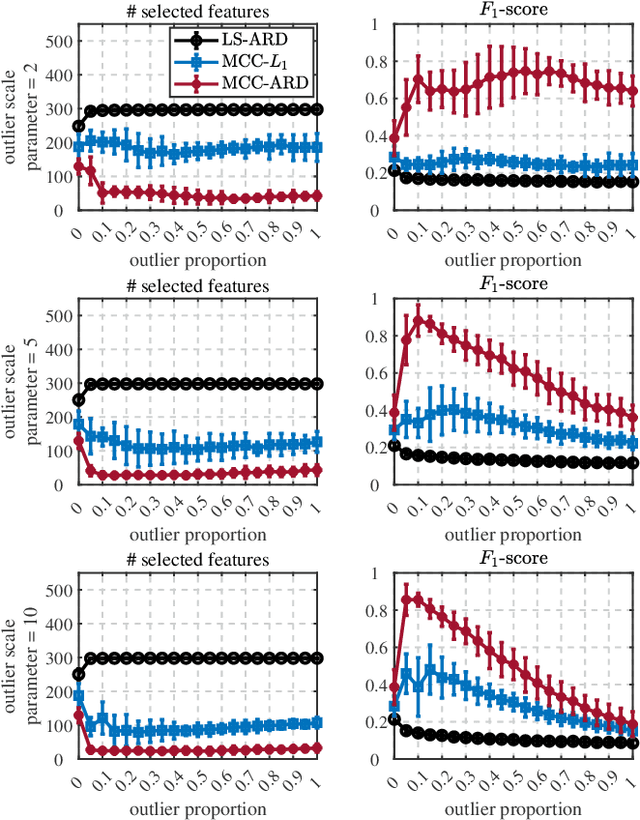
Sparseness and robustness are two important properties for many machine learning scenarios. In the present study, regarding the maximum correntropy criterion (MCC) based robust regression algorithm, we investigate to integrate the MCC method with the automatic relevance determination (ARD) technique in a Bayesian framework, so that MCC-based robust regression could be implemented with adaptive sparseness. To be specific, we use an inherent noise assumption from the MCC to derive an explicit likelihood function, and realize the maximum a posteriori (MAP) estimation with the ARD prior by variational Bayesian inference. Compared to the existing robust and sparse L1-regularized MCC regression, the proposed MCC-ARD regression can eradicate the troublesome tuning for the regularization hyper-parameter which controls the regularization strength. Further, MCC-ARD achieves superior prediction performance and feature selection capability than L1-regularized MCC, as demonstrated by a noisy and high-dimensional simulation study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge