Adaptive Regularized Low-Rank Tensor Decomposition for Hyperspectral Image Denoising and Destriping
Paper and Code
Jan 11, 2024

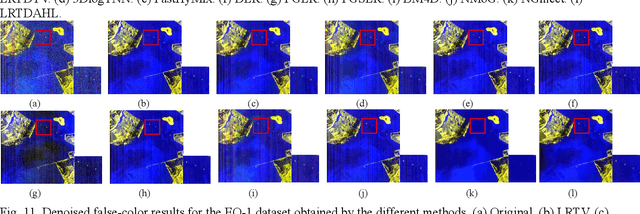

Hyperspectral images (HSIs) are inevitably degraded by a mixture of various types of noise, such as Gaussian noise, impulse noise, stripe noise, and dead pixels, which greatly limits the subsequent applications. Although various denoising methods have already been developed, accurately recovering the spatial-spectral structure of HSIs remains a challenging problem to be addressed. Furthermore, serious stripe noise, which is common in real HSIs, is still not fully separated by the previous models. In this paper, we propose an adaptive hyperLaplacian regularized low-rank tensor decomposition (LRTDAHL) method for HSI denoising and destriping. On the one hand, the stripe noise is separately modeled by the tensor decomposition, which can effectively encode the spatial-spectral correlation of the stripe noise. On the other hand, adaptive hyper-Laplacian spatial-spectral regularization is introduced to represent the distribution structure of different HSI gradient data by adaptively estimating the optimal hyper-Laplacian parameter, which can reduce the spatial information loss and over-smoothing caused by the previous total variation regularization. The proposed model is solved using the alternating direction method of multipliers (ADMM) algorithm. Extensive simulation and real-data experiments all demonstrate the effectiveness and superiority of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge