Adaptive Multi-View ICA: Estimation of noise levels for optimal inference
Paper and Code
Feb 22, 2021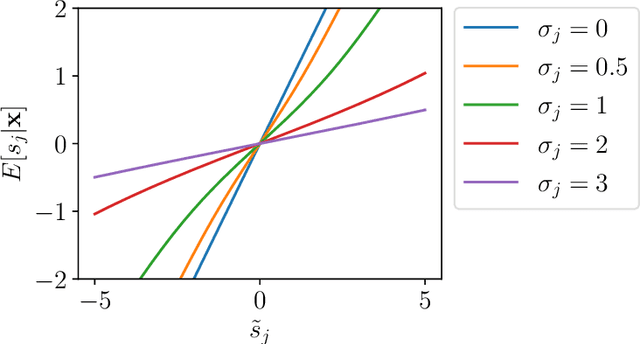
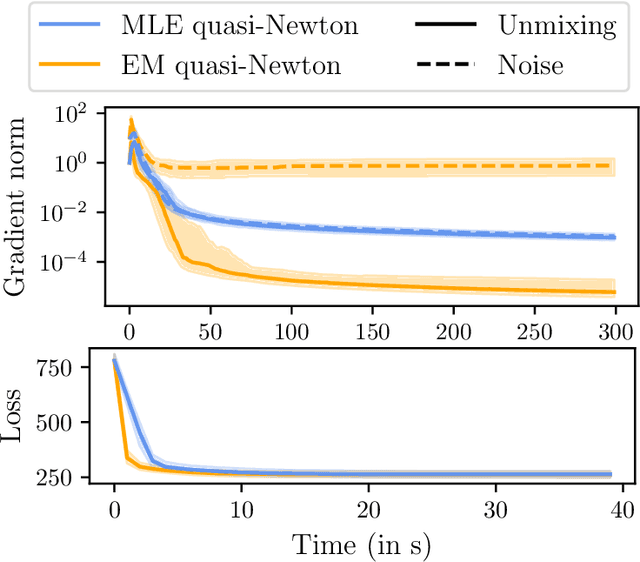
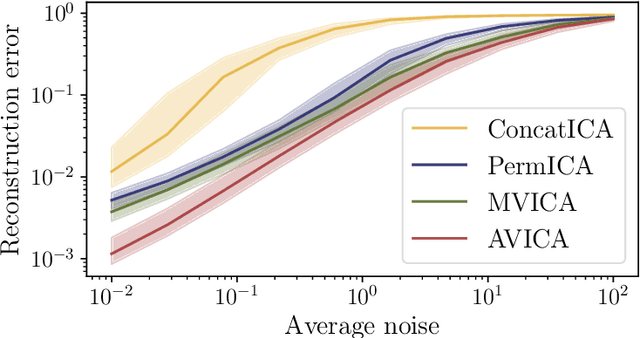
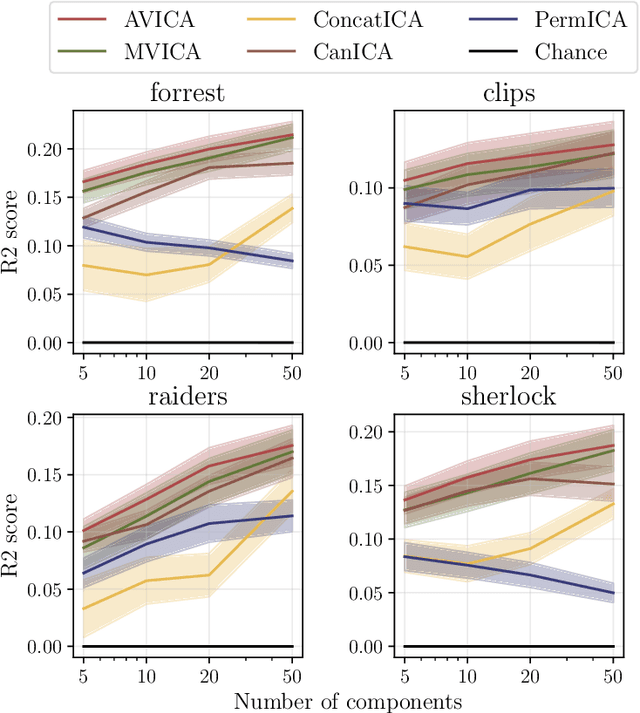
We consider a multi-view learning problem known as group independent component analysis (group ICA), where the goal is to recover shared independent sources from many views. The statistical modeling of this problem requires to take noise into account. When the model includes additive noise on the observations, the likelihood is intractable. By contrast, we propose Adaptive multiView ICA (AVICA), a noisy ICA model where each view is a linear mixture of shared independent sources with additive noise on the sources. In this setting, the likelihood has a tractable expression, which enables either direct optimization of the log-likelihood using a quasi-Newton method, or generalized EM. Importantly, we consider that the noise levels are also parameters that are learned from the data. This enables sources estimation with a closed-form Minimum Mean Squared Error (MMSE) estimator which weights each view according to its relative noise level. On synthetic data, AVICA yields better sources estimates than other group ICA methods thanks to its explicit MMSE estimator. On real magnetoencephalograpy (MEG) data, we provide evidence that the decomposition is less sensitive to sampling noise and that the noise variance estimates are biologically plausible. Lastly, on functional magnetic resonance imaging (fMRI) data, AVICA exhibits best performance in transferring information across views.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge