Adaptive Message Quantization and Parallelization for Distributed Full-graph GNN Training
Paper and Code
Jun 02, 2023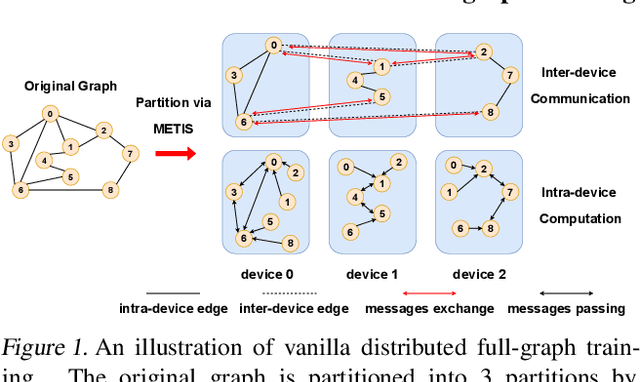
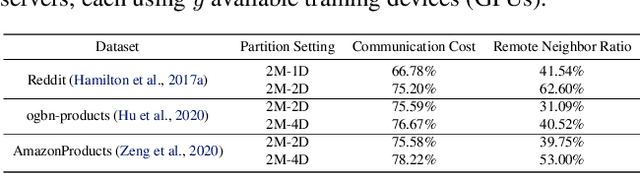
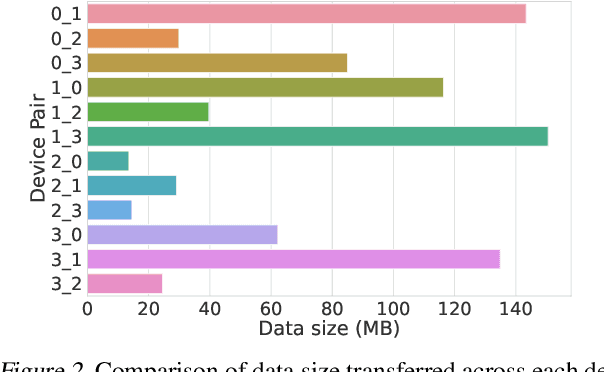
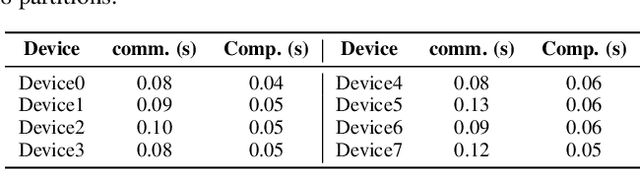
Distributed full-graph training of Graph Neural Networks (GNNs) over large graphs is bandwidth-demanding and time-consuming. Frequent exchanges of node features, embeddings and embedding gradients (all referred to as messages) across devices bring significant communication overhead for nodes with remote neighbors on other devices (marginal nodes) and unnecessary waiting time for nodes without remote neighbors (central nodes) in the training graph. This paper proposes an efficient GNN training system, AdaQP, to expedite distributed full-graph GNN training. We stochastically quantize messages transferred across devices to lower-precision integers for communication traffic reduction and advocate communication-computation parallelization between marginal nodes and central nodes. We provide theoretical analysis to prove fast training convergence (at the rate of O(T^{-1}) with T being the total number of training epochs) and design an adaptive quantization bit-width assignment scheme for each message based on the analysis, targeting a good trade-off between training convergence and efficiency. Extensive experiments on mainstream graph datasets show that AdaQP substantially improves distributed full-graph training's throughput (up to 3.01 X) with negligible accuracy drop (at most 0.30%) or even accuracy improvement (up to 0.19%) in most cases, showing significant advantages over the state-of-the-art works.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge