Adaptive Low-Pass Filtering using Sliding Window Gaussian Processes
Paper and Code
Nov 05, 2021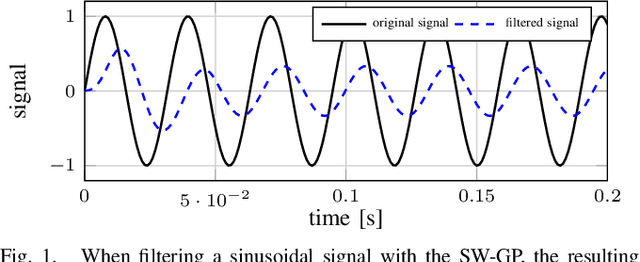
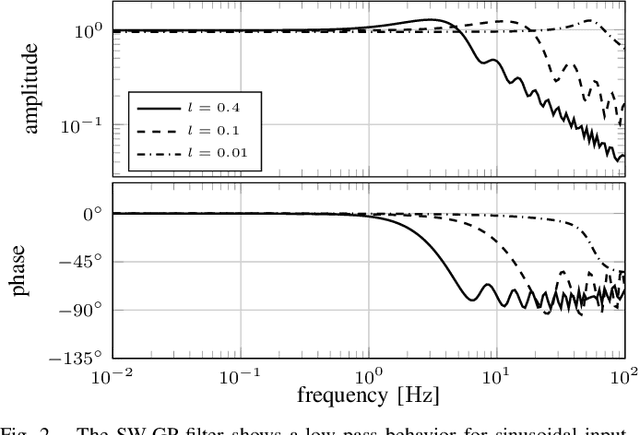
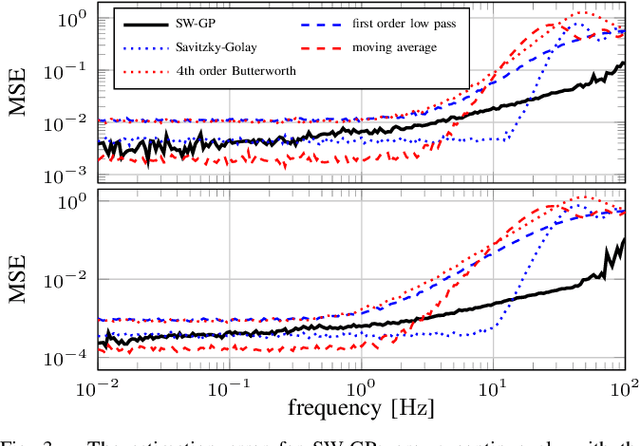
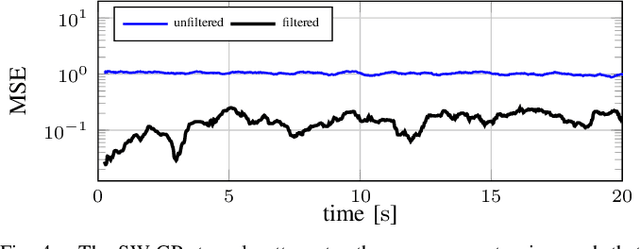
When signals are measured through physical sensors, they are perturbed by noise. To reduce noise, low-pass filters are commonly employed in order to attenuate high frequency components in the incoming signal, regardless if they come from noise or the actual signal. Therefore, low-pass filters must be carefully tuned in order to avoid significant deterioration of the signal. This tuning requires prior knowledge about the signal, which is often not available in applications such as reinforcement learning or learning-based control. In order to overcome this limitation, we propose an adaptive low-pass filter based on Gaussian process regression. By considering a constant window of previous observations, updates and predictions fast enough for real-world filtering applications can be realized. Moreover, the online optimization of hyperparameters leads to an adaptation of the low-pass behavior, such that no prior tuning is necessary. We show that the estimation error of the proposed method is uniformly bounded, and demonstrate the flexibility and efficiency of the approach in several simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge