Adaptive Hierarchical Similarity Metric Learning with Noisy Labels

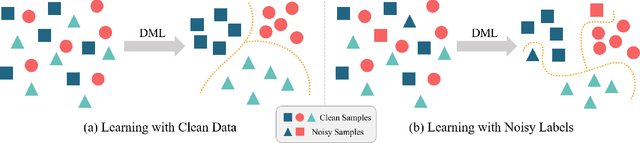
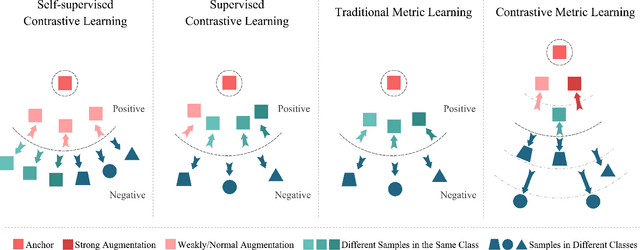
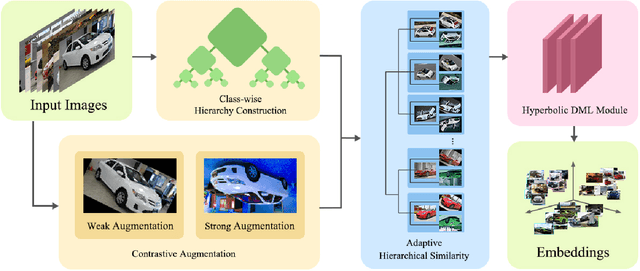
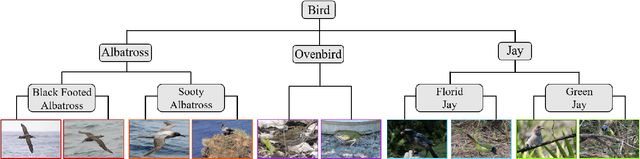
Deep Metric Learning (DML) plays a critical role in various machine learning tasks. However, most existing deep metric learning methods with binary similarity are sensitive to noisy labels, which are widely present in real-world data. Since these noisy labels often cause severe performance degradation, it is crucial to enhance the robustness and generalization ability of DML. In this paper, we propose an Adaptive Hierarchical Similarity Metric Learning method. It considers two noise-insensitive information, \textit{i.e.}, class-wise divergence and sample-wise consistency. Specifically, class-wise divergence can effectively excavate richer similarity information beyond binary in modeling by taking advantage of Hyperbolic metric learning, while sample-wise consistency can further improve the generalization ability of the model using contrastive augmentation. More importantly, we design an adaptive strategy to integrate this information in a unified view. It is noteworthy that the new method can be extended to any pair-based metric loss. Extensive experimental results on benchmark datasets demonstrate that our method achieves state-of-the-art performance compared with current deep metric learning approaches.