Adaptive Hedging under Delayed Feedback
Paper and Code
Feb 27, 2019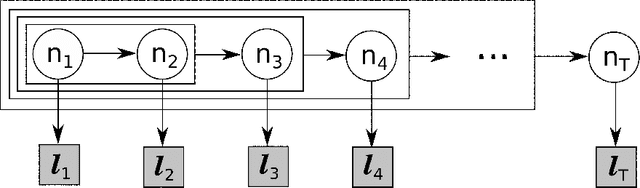
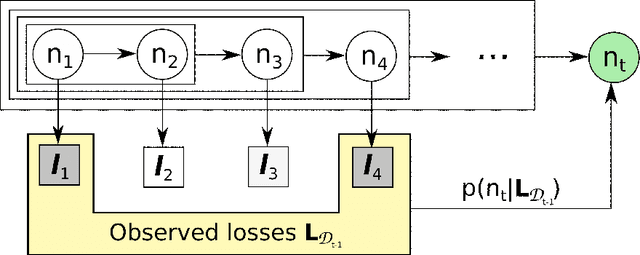
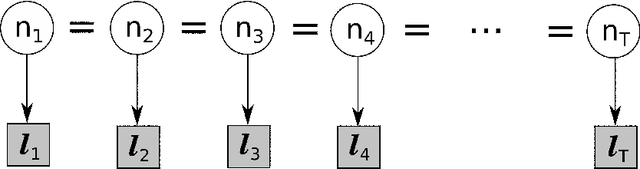
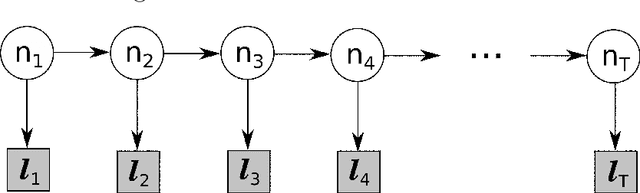
The article is devoted to investigating the application of hedging strategies to online expert weight allocation under delayed feedback. As the main result, we develop the General Hedging algorithm $\mathcal{G}$ based on the exponential reweighing of experts' losses. We build the artificial probabilistic framework and use it to prove the adversarial loss bounds for the algorithm $\mathcal{G}$ in the delayed feedback setting. The designed algorithm $\mathcal{G}$ can be applied to both countable and continuous sets of experts. We also show how algorithm $\mathcal{G}$ extends classical Hedge (Multiplicative Weights) and adaptive Fixed Share algorithms to the delayed feedback and derive their regret bounds for the delayed setting by using our main result.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge