Adaptive Explicit Kernel Minkowski Weighted K-means
Paper and Code
Dec 04, 2020
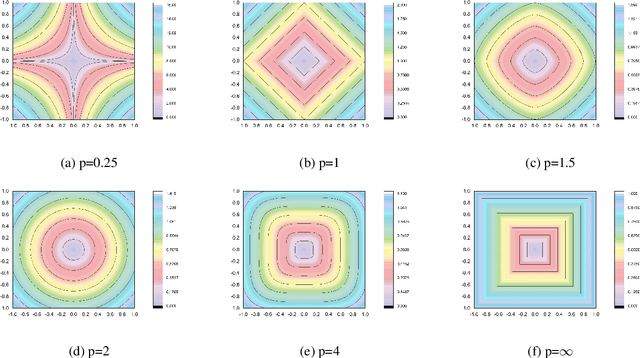
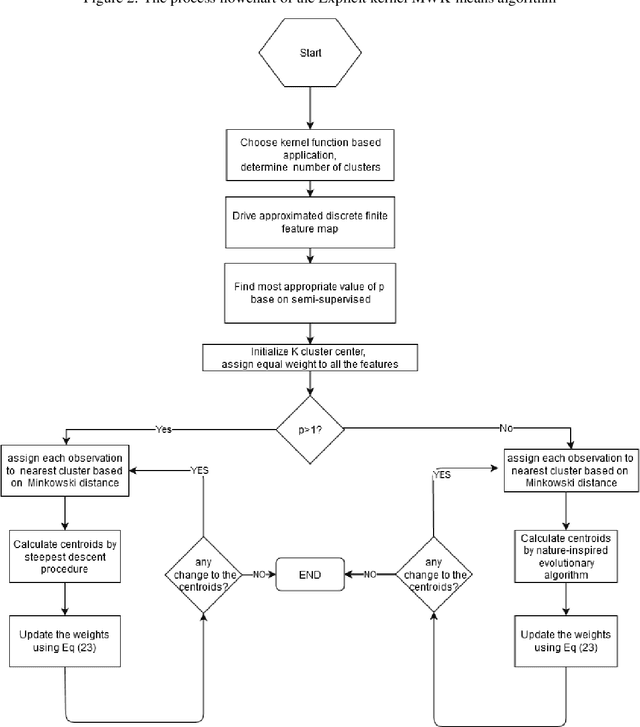
The K-means algorithm is among the most commonly used data clustering methods. However, the regular K-means can only be applied in the input space and it is applicable when clusters are linearly separable. The kernel K-means, which extends K-means into the kernel space, is able to capture nonlinear structures and identify arbitrarily shaped clusters. However, kernel methods often operate on the kernel matrix of the data, which scale poorly with the size of the matrix or suffer from the high clustering cost due to the repetitive calculations of kernel values. Another issue is that algorithms access the data only through evaluations of $K(x_i, x_j)$, which limits many processes that can be done on data through the clustering task. This paper proposes a method to combine the advantages of the linear and nonlinear approaches by using driven corresponding approximate finite-dimensional feature maps based on spectral analysis. Applying approximate finite-dimensional feature maps were only discussed in the Support Vector Machines (SVM) problems before. We suggest using this method in kernel K-means era as alleviates storing huge kernel matrix in memory, further calculating cluster centers more efficiently and access the data explicitly in feature space. These explicit feature maps enable us to access the data in the feature space explicitly and take advantage of K-means extensions in that space. We demonstrate our Explicit Kernel Minkowski Weighted K-mean (Explicit KMWK-mean) method is able to be more adopted and find best-fitting values in new space by applying additional Minkowski exponent and feature weights parameter. Moreover, it can reduce the impact of concentration on nearest neighbour search by suggesting investigate among other norms instead of Euclidean norm, includes Minkowski norms and fractional norms (as an extension of the Minkowski norms with p<1).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge