Adaptive Constraint Partition based Optimization Framework for Large-scale Integer Linear Programming(Student Abstract)
Paper and Code
Nov 18, 2022
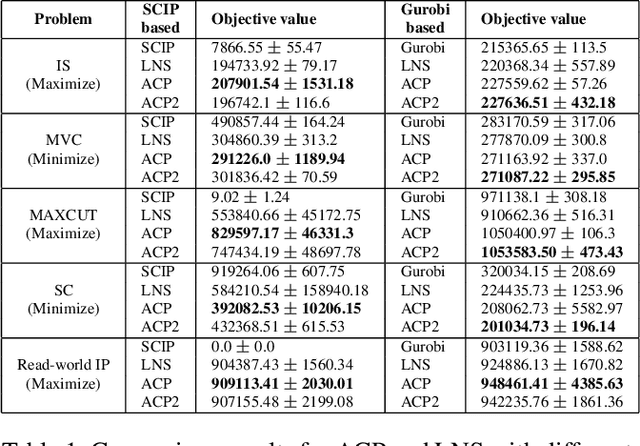

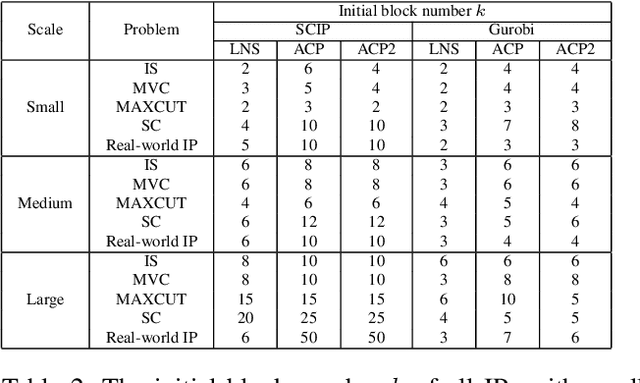
Integer programming problems (IPs) are challenging to be solved efficiently due to the NP-hardness, especially for large-scale IPs. To solve this type of IPs, Large neighborhood search (LNS) uses an initial feasible solution and iteratively improves it by searching a large neighborhood around the current solution. However, LNS easily steps into local optima and ignores the correlation between variables to be optimized, leading to compromised performance. This paper presents a general adaptive constraint partition-based optimization framework (ACP) for large-scale IPs that can efficiently use any existing optimization solver as a subroutine. Specifically, ACP first randomly partitions the constraints into blocks, where the number of blocks is adaptively adjusted to avoid local optima. Then, ACP uses a subroutine solver to optimize the decision variables in a randomly selected block of constraints to enhance the variable correlation. ACP is compared with LNS framework with different subroutine solvers on four IPs and a real-world IP. The experimental results demonstrate that in specified wall-clock time ACP shows better performance than SCIP and Gurobi.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge