Adaptive Approximation and Estimation of Deep Neural Network to Intrinsic Dimensionality

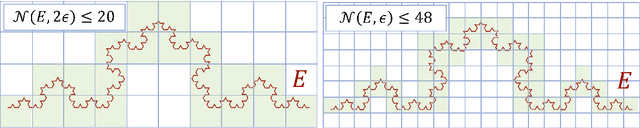
We theoretically prove that the generalization performance of deep neural networks (DNNs) is mainly determined by an intrinsic low-dimensional structure of data. Recently, DNNs empirically provide outstanding performance in various machine learning applications. Motivated by the success, theoretical properties of DNNs (e.g. a generalization error) are actively investigated by numerous studies toward understanding their mechanism. Especially, how DNNs behave with high-dimensional data is one of the most important concerns. However, the problem is not sufficiently investigated from an aspect of characteristics of data, despite it is frequently observed that high-dimensional data have an intrinsic low-dimensionality in practice. In this paper, to clarify a connection between DNNs and such the data, we derive bounds for approximation and generalization errors by DNNs with intrinsic low-dimensional data. To the end, we introduce a general notion of an intrinsic dimension and develop a novel proof technique to evaluate the errors. Consequently, we show that convergence rates of the errors by DNNs do not depend on the nominal high-dimensionality of data, but depend on the lower intrinsic dimension. We also show that the rate is optimal in the minimax sense. Furthermore, we find that DNNs with increasing layers can handle a broader class of intrinsic low-dimensional data. We conduct a numerical simulation to validate (i) the intrinsic dimension of data affects the generalization error of DNNs, and (ii) DNNs outperform other non-parametric estimators which are also adaptive to the intrinsic dimension.