Active Contour with A Tangential Component
Paper and Code
Apr 29, 2012

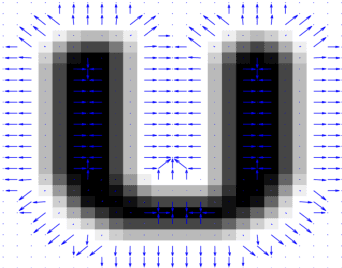
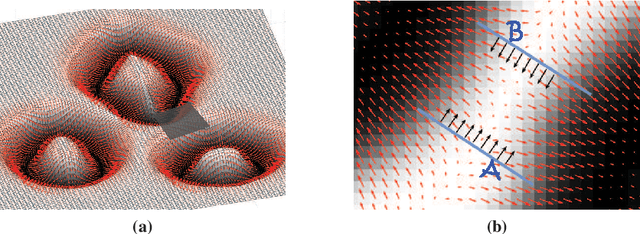
Conventional edge-based active contours often require the normal component of an edge indicator function on the optimal contours to approximate zero, while the tangential component can still be significant. In real images, the full gradients of the edge indicator function along the object boundaries are often small. Hence, the curve evolution of edge-based active contours can terminate early before converging to the object boundaries with a careless contour initialization. We propose a novel Geodesic Snakes (GeoSnakes) active contour that requires the full gradients of the edge indicator to vanish at the optimal solution. Besides, the conventional curve evolution approach for minimizing active contour energy cannot fully solve the Euler-Lagrange (EL) equation of our GeoSnakes active contour, causing a Pseudo Stationary Phenomenon (PSP). To address the PSP problem, we propose an auxiliary curve evolution equation, named the equilibrium flow (EF) equation. Based on the EF and the conventional curve evolution, we obtain a solution to the full EL equation of GeoSnakes active contour. Experimental results validate the proposed geometrical interpretation of the early termination problem, and they also show that the proposed method overcomes the problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge